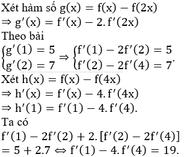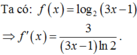a) Với \({x_0}\) bất kì, ta có:

\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)

Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)

b) \(y' = \left( {{x^n}} \right)' = n{x^{n - 1}}\)

Chọn D.

\(x'\cdot\left(x+2\right)^3+x\left[\left(x+2\right)^3\right]'\)

\(=1\cdot\left(x+2\right)^3+x\cdot3\left(x+2\right)^2+\left(x+2\right)'\)

\(=\left(x+2\right)^3+3x\left(x+2\right)^2\)

\(=\left(x+2\right)^2\left(4x+2\right)\)

a: \(y'=\left(x\cdot log_2x\right)'=log_2x+x\cdot\dfrac{1}{x\cdot ln2}=log_2x+\dfrac{1}{ln2}\)

b: \(y'=\left(x^3e^x\right)'=\left(x^3\right)'\cdot e^x+x^3\cdot\left(e^x\right)'\)

\(=3x^2\cdot e^x+x^3\cdot e^x\)

Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì

\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\) 

\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)

Từ đó ta dễ dàng tổng quát được:

 \(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)

Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)

Áp dụng công thức trên ta được:

\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)

Bạn tự rút gọn kết quả nhé

\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?

Đáp án D

Ta có: \(y' = {\left( {\tan x} \right)^\prime } = \frac{1}{{{{\cos }^2}x}}\)

Vậy \(y'\left( {\frac{{3\pi }}{4}} \right) = \frac{1}{{{{\cos }^2}\left( {\frac{{3\pi }}{4}} \right)}} = 2\).

tham khảo:

a)\(y'=\dfrac{d}{dx}\left(x^3\right)-\dfrac{d}{dx}\left(3x^2\right)+\dfrac{d}{dx}\left(2x\right)+\dfrac{d}{dx}\left(1\right)\)

\(y'=3x^2-6x+2\)

b)\(\dfrac{d}{dx}\left(x^n\right)=nx^{n-1}\)

\(\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}}\)

\(\dfrac{d}{dx}\left(f\left(x\right)+g\left(x\right)\right)=f'\left(x\right)+g'\left(x\right)\)

\(\dfrac{d}{dx}\left(cf\left(x\right)\right)=cf'\left(x\right)\)

\(y'=\dfrac{d}{dx}\left(x^2\right)-\dfrac{d}{dx}\left(4\sqrt{x}\right)+\dfrac{d}{dx}\left(3\right)\)

\(y'=2x-2\sqrt{x}\)