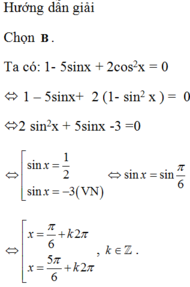Sin5x/5sinx=1

Những câu hỏi liên quan
Giải phương trình \(\dfrac{Sin5x}{5Sinx}=1\)
<=> sin5x=5sinx
<=> Sin5x-sinx=4sinx
<=> 2cos3x.sin2x=4sinx
<=>4cos3x.sinx.cosx=4sinx
<=>(cos3x.cosx-1).sinx=0
Sinx=0 hoặc cos3x.cosx -1=0
TH1. Sinx=0 => x=kπ
TH2: cos3x.cosx-1=0
<=> Cos3x.cosx=1
<=>cos4x + cos2x =2
<=> 2cos ²2x -1 +cos2x -2=0
<=> 2cos ²2x +cos 2x -3=0
Cos 2x= 1 =>. X=kπ/2
Cos2x= -3/2 <-1(loai)
Vậy x=kπ/2
Đúng 0
Bình luận (0)
ĐK: \(x\ne k\pi\)
\(\dfrac{sin5x}{5sinx}=1\)
\(\Leftrightarrow sin5x=5sinx\)
\(\Leftrightarrow sin5x-sinx=4sinx\)
\(\Leftrightarrow2cos3x.sin2x=4sinx\)
\(\Leftrightarrow4sinx.cosx.cos3x=4sinx\)
\(\Leftrightarrow cosx.cos3x=1\) (Vì \(sinx\ne0\))
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x+cos2x\right)=1\)
\(\Leftrightarrow2cos^22x-1+cos2x=2\)
\(\Leftrightarrow2cos^22x+cos2x-3=0\)
\(\Leftrightarrow\left(cos2x-1\right)\left(2cos2x+3\right)=0\)
\(\Leftrightarrow cos2x=1\) (Vì \(2cos2x+3>0\))
\(\Leftrightarrow x=k\pi\left(l\right)\)
Vậy phương trình đã cho vô nghiệm
Đúng 0
Bình luận (0)
giải pt :
a, cos(2x+\(\frac{\pi}{3}\)) =\(\frac{-\sqrt{2}}{2}\)
b, 3cos2x +5sinx -5sinx -5 =0
c, cos4x -2sin2x -1 =0
d, sin5x -cos5x +1 = 0
e, 2cos2 - sinx - cos x -2sin2x - 1 = 0
f, cos ( 4x + \(\frac{\pi}{3}\)) = sin (x +\(\frac{\pi}{5}\))
giải giúp t vs t đag cần
thank you.
a, ta có 2x + π/3 = 3π/4 +k2π hoặc 2x + π/3 = -3π/4 + k2π
=> x= 5π/24 + kπ hoặc x= -13π/24 +kπ
b, đề sai phải ko
c, cos22x - sin22x - 2sinx -1=0
<=> -2sin22x -2sin2x =0
<=> sin2x=0 hoặc sin2x=-1
<=> x=kπ hoặc x= π/2 + kπ ; x=-π/4 +kπ hoặc x=5π/8 + kπ
d, cos5xcosπ/4 - sin5xsinπ/4 = -1/2
cos( 5x + π/4 ) = -1/2
<=> x=π/12 +k2π/5 hoặc x= -11π/60 + k2π/5
f,4x+π/3=3π/10 -x +k2π hoặc 4x+π/3 = x - 3π/10 +k2π
<=> x =-π/150 + k2π/5 hoặc x = π/90 +k2π/3
Đúng 0
Bình luận (0)
1+sin5x=2cos22×x/2
Sin5x=sin4x-cos4x
Câu đầu đơn giản là ko dịch được \(cos^22\times x/2\) nghĩa là gì :)
\(sin5x=\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)\)
\(\Leftrightarrow sin5x=-\left(cos^2x-sin^2x\right)\)
\(\Leftrightarrow sin5x=-cos2x\)
\(\Leftrightarrow sin5x=sin\left(2x-\frac{\pi}{2}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=2x-\frac{\pi}{2}+k2\pi\\5x=\frac{3\pi}{2}-2x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Đúng 0
Bình luận (0)
\(1+sin5x=2cos^2\frac{x}{2}\)
\(\Leftrightarrow sin5x=2cos^2\frac{x}{2}-1\)
\(\Leftrightarrow sin5x=cosx\)
\(\Leftrightarrow sin5x=sin\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\frac{\pi}{2}-x+k2\pi\\5x=\frac{\pi}{2}+x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
sin3x + 1=2sin22x
sin2xcos3x = sin5x
cos5x + cos3x + sin2x =0
sin5x + 1 = 2sin2x
sin3xcosx + 2cos22x = 1 + cos3xsinx
sin3x + 1=2sin22x
<=> sin3x + 1 = 2\(\dfrac{1-cos4x}{2}\)
<=> sin3x + 1 = 1 - cos4x
<=> sin3x = -cos4x
<=> sin3x + cos4x = 0
<=> \(\dfrac{\sqrt{2}}{2}\)sin3x + \(\dfrac{\sqrt{2}}{2}\)cos4x = 0 (chia 2 vế cho \(\sqrt{2}\)).
<=> cos\(\dfrac{\pi}{4}\)sin3x + sin\(\dfrac{\pi}{4}\)cos4x = 0
<=> sin (3x+\(\dfrac{\pi}{4}\)) = 0
<=> sin(3x+\(\dfrac{\pi}{4}\)) = sin0
<=> \(\left[{}\begin{matrix}3x+\dfrac{\pi}{4}=0+k2\pi\\3x+\dfrac{\pi}{4}=\pi-0+k2\pi\end{matrix}\right.\)(k\(\in\)Z)
<=>\(\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+\dfrac{k2\pi}{3}\\x=\dfrac{5\pi}{12}+\dfrac{k2\pi}{3}\end{matrix}\right.\)(k\(\in\)Z)
Đúng 0
Bình luận (0)
\(sin5x+sinx+2sin^2x=1\)
\(\Leftrightarrow sin5x+sinx-\left(1-2sin^2x\right)=0\)
\(\Leftrightarrow2sin3x.cos2x-cos2x=0\)
\(\Leftrightarrow cos2x\left(2sin3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin3x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\3x=\dfrac{\pi}{6}+k2\pi\\3x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\\x=\dfrac{5\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(sin5x+sinx+2sin^2x=1\)
\(\Leftrightarrow\left(sin5x+sinx\right)-\left(1-2sin^2x\right)=0\)
\(\Leftrightarrow2sin3x.cos2x-cos2x=0\)
\(\Leftrightarrow cos2x\left(2sin3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin3x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}+k\pi\\\left[{}\begin{matrix}3x=\dfrac{\pi}{6}+k2\pi\\3x=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\end{matrix}\right.\)
Vậy...
Đúng 1
Bình luận (0)
\(sin5x+sinx+2sin^2x=1\)
\(\Leftrightarrow2sin3x.cos2x-cos2x=0\)
\(\Leftrightarrow cos2x\left(2sin3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\sin3x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=\dfrac{5\pi}{18}+\dfrac{k2\pi}{3}\\x=\dfrac{\pi}{18}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Nghiệm của phương trình 1 – 5sinx + 2cos2x 0 là
Đọc tiếp
Nghiệm của phương trình 1 – 5sinx + 2cos2x =0 là
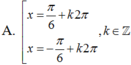

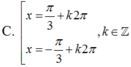
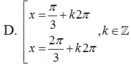
Giải phương trình sau: 5sinx – 2 3(1 – sinx)tan2x A. x
π
6
+ k2π B. x
5
π
6
+ kπ C. x
-
5
π
6
+ kπ, kπ D. Đáp án khác.
Đọc tiếp
Giải phương trình sau: 5sinx – 2 = 3(1 – sinx)tan2x
A. x = π 6 + k2π
B. x = 5 π 6 + kπ
C. x = - 5 π 6 + kπ, kπ
D. Đáp án khác.
a, cos4x + 12sin2x -1 0
b, cos4x - sin4x + cos4x 0
c, 5.(sinx + dfrac{cos3x+sin3x}{1+2sin2x} ) 3 + cos2x với mọi xinleft(0;2piright)
d, dfrac{sin3x}{3}dfrac{sin5x}{5}
e, dfrac{sin5x}{5sinx}1
f, cos23x - cos2x - cos2x 0
g, cos4x + sin4x + cos(x-dfrac{pi}{4} ) . sin(3x-dfrac{pi}{4} ) - dfrac{3}{2} 0
h, sinleft(2x+dfrac{5pi}{2}right) - 3cosleft(x-dfrac{7pi}{2}right) 1 + 2sinx với xinleft(dfrac{pi}{2};2piright)
i, 5sinx - 2 3.( 1- sinx ) . tan3x
k, ( sin2x + sqrt{3}cos2x)2 - 5 cos le...
Đọc tiếp
a, cos4x + 12sin2x -1 = 0
b, cos4x - sin4x + cos4x = 0
c, 5.(sinx + \(\dfrac{cos3x+sin3x}{1+2sin2x}\) ) = 3 + cos2x với mọi x\(\in\left(0;2\pi\right)\)
d, \(\dfrac{sin3x}{3}=\dfrac{sin5x}{5}\)
e, \(\dfrac{sin5x}{5sinx}=1\)
f, cos23x - cos2x - cos2x =0
g, cos4x + sin4x + cos(\(x-\dfrac{\pi}{4}\) ) . sin(\(3x-\dfrac{\pi}{4}\) ) - \(\dfrac{3}{2}\) = 0
h, sin\(\left(2x+\dfrac{5\pi}{2}\right)\) - 3cos\(\left(x-\dfrac{7\pi}{2}\right)\)= 1 + 2sinx với x\(\in\left(\dfrac{\pi}{2};2\pi\right)\)
i, 5sinx - 2 = 3.( 1- sinx ) . tan3x
k, ( sin2x + \(\sqrt{3}cos2x\))2 - 5 = cos \(\left(2x-\dfrac{\pi}{6}\right)\)
l, \(\dfrac{2.\left(cos^6x+sin^6x\right)-sinx.cosx}{\sqrt{2}-2sinx}=0\)
m, \(\dfrac{\left(1+sinx+cos2x\right).sin\left(x+\dfrac{\pi}{4}\right)}{1+tanx}=\dfrac{1}{\sqrt{2}}cosx\)
Mọi người giúp mình nha ! Mình cần gấp cho ngày mai ![]()
sin5x+sin3x+2cos2=1+sin4x
\(\sin\left(5x\right)+\sin\left(3x\right)+2\cos\left(x\right)=1+\sin\left(4x\right)\)
\(\Leftrightarrow2\sin\left(4x\right)\cos\left(x\right)-\sin\left(4x\right)+2\cos\left(x\right)-1=0\)
\(\Leftrightarrow\sin\left(4x\right)(2\cos\left(x\right)-1)+(2\cos\left(x\right)-1)=0\)
\(\Leftrightarrow(2\cos\left(x\right)-1)(\sin\left(4x\right)+1)=0\)
\(\Rightarrow\left[{}\begin{matrix}\cos\left(x\right)=\dfrac{1}{2}\\\sin\left(4x\right)=-1\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\4x=\dfrac{-\pi}{2}+k2\pi\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\pm\dfrac{\pi}{3}+k2\pi\\x=\dfrac{-\pi}{8}+k\dfrac{\pi}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)