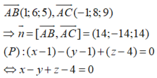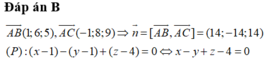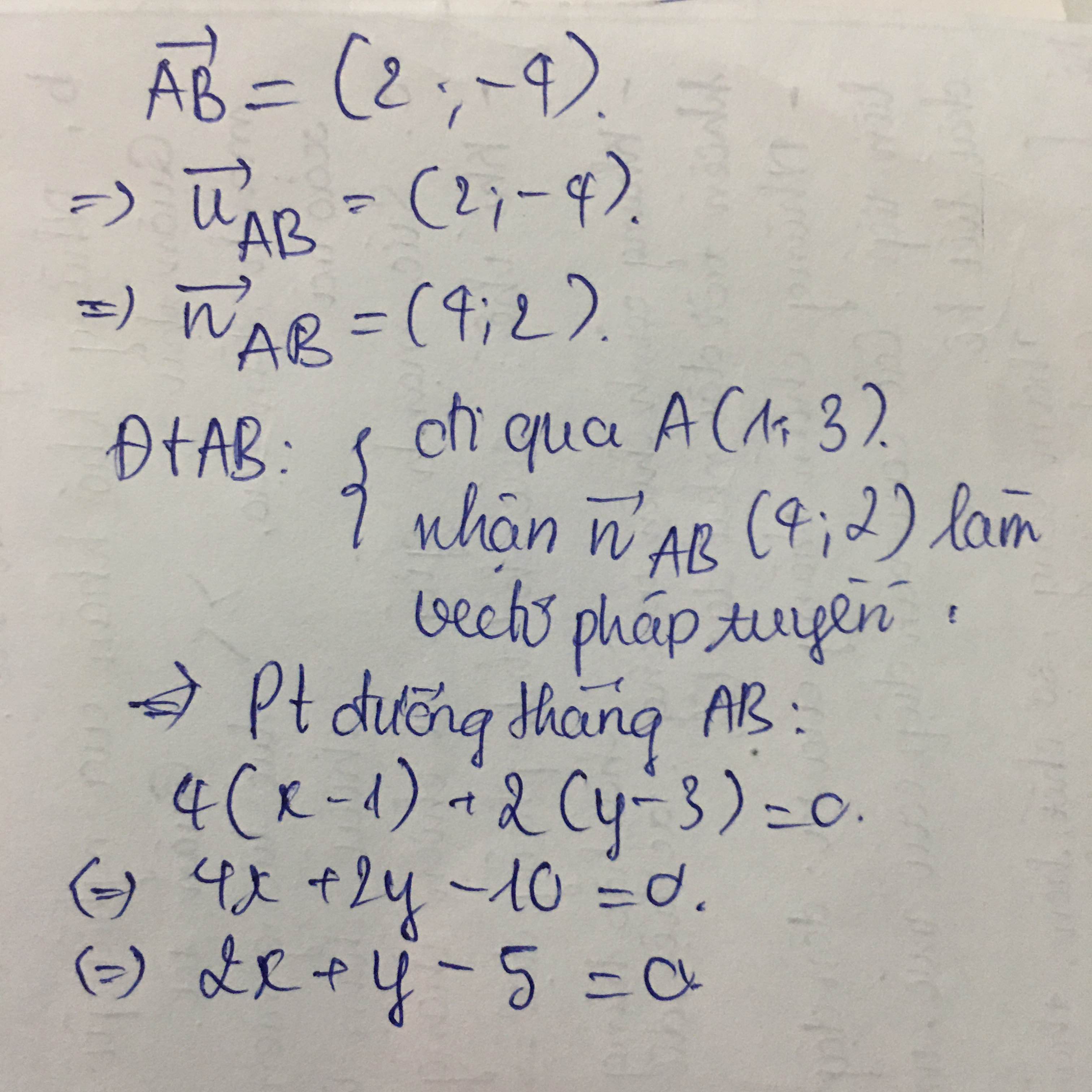viết phương trình mặt phẳng đi qua điểm N(-3;1;2) và chứa trục Oz

Những câu hỏi liên quan
Viết phương trình mặt phẳng:
Đi qua điểm M(1; -2; 4) và nhận n → = (2 ; 3 ; 5) làm vec tơ pháp tuyến
Mặt phẳng đi qua điểm M(1; -2; 4) và nhận n → = (2; 3; 5) làm vectơ pháp tuyến là:
2(x – 1) + 3(y + 2) + 5(z – 4) = 0
⇔ 2x + 3y + 5z – 16 = 0.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, viết phương trình tham số của đường thẳng đi qua hai điểm M(3;-1) và N(4;1)
vecto MN=(1;2)
=>VTPT là (-2;1)
Phương trình MN là:
-2(x-3)+1(y+1)=0
=>-2x+6+y+1=0
=>-2x+y+7=0
Phương trình tham số là:
x=3+t và y=-1+2t
Đúng 1
Bình luận (0)
Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13) A. 2x+y+z+10 B. x-y +z-40 C. 7x-2y+z-90 D. 2x+y-z-20
Đọc tiếp
Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13)
A. 2x+y+z+1=0
B. x-y +z-4=0
C. 7x-2y+z-9=0
D. 2x+y-z-2=0
Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13) A.
2
x
+
y
+
z
+
1
0.
B.
x
−
y
+
z
−
4
0.
C.
7
x
−...
Đọc tiếp
Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13)
A. 2 x + y + z + 1 = 0.
B. x − y + z − 4 = 0.
C. 7 x − 2 y + z − 9 = 0.
D. 2 x + y − z − 2 = 0.
Viết phương trình mặt phẳng đi qua 3 điểm A(1;1;4), B(2;7;9), C(0;9;13)
A. 2x + y + z + 1=0
B. x - y + z - 4 = 0
C. 7x - 2y + z - 9 = 0
D. 2x + y - z - 2 =0
Trong mặt phẳng 0xy cho A(-1;2)
a)Viết phương trình đường thẳng (d) đi qua A và có hệ số góc là -3. Vẽ (d)
b)Viết phương trình đường thẳng (d1) đi qua M( 2;3) và N(4;5)
c)Tìm tọa độ giao điểm (d) và (d1)
a: Vì (d) có hệ số góc là -3 nên a=-3
Vậy: (d): y=-3x+b
Thay x=-1 và y=2 vào (d), ta được:
b+3=2
hay b=-1
Đúng 0
Bình luận (1)
\(a,\) Gọi \(\left(d\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}-a+b=2\\a=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-1\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x-1\)
\(b,\) Gọi \(\left(d_1\right):y=ax+b\left(a\ne0\right)\) là đt cần tìm
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=3\\4a+b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=x+1\)
\(c,PTHDGD:-3x-1=x+1\Leftrightarrow x=-\dfrac{1}{2}\Leftrightarrow y=\dfrac{1}{2}\Leftrightarrow B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\\ \text{Vậy }B\left(-\dfrac{1}{2};\dfrac{1}{2}\right)\text{ là giao 2 đths}\)
Đúng 1
Bình luận (0)
Viết phương trình mặt phẳng ( α ) trong các trường hợp sau: ( α ) đi qua ba điểm M(1; 1; 1), N(4; 3; 2), P(5; 2; 1).
Hai vecto có giá song song hoặc nằm trên ( α ) là: MN → = (3; 2; 1) và MP → = (4; 1; 0).
Suy ra ( α ) có vecto pháp tuyến là n → = MN → ∧ MP → = (−1; 4; −5)
Vậy phương trình của ( α ) là: -1(x – 1) + 4(y – 1) – 5(z – 1) = 0 hay x – 4y + 5z – 2 = 0
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho ba điểm A(1;3); B(3;-1) và C(-2; 3).
a. Viết phương trình qua hai điểm A, B.
b. Viết phương trình đường thẳng d đi qua C, đồng thơi d cách đều A và B.
viết phương trình mặt phẳng (P) đi qua 3 điểm A(1;2;3),B(2;3;1)và C(3;1;2)
viết phương trình mặt phẳng đi qua M(3;4;-5) và có cặp vectơ chỉ phưowng trình u⃗ =(3;1;−1),v⃗ =(1;−2;1)
\(\left[\overrightarrow{AB};\overrightarrow{AC}\right]=\left(\left|\begin{matrix}1&-2\\-1&-1\end{matrix}\right|;\left|\begin{matrix}-2&1\\-1&2\end{matrix}\right|;\left|\begin{matrix}1&1\\2&-1\end{matrix}\right|\right)=-3\left(1;1;1\right)\)
Đúng 0
Bình luận (0)