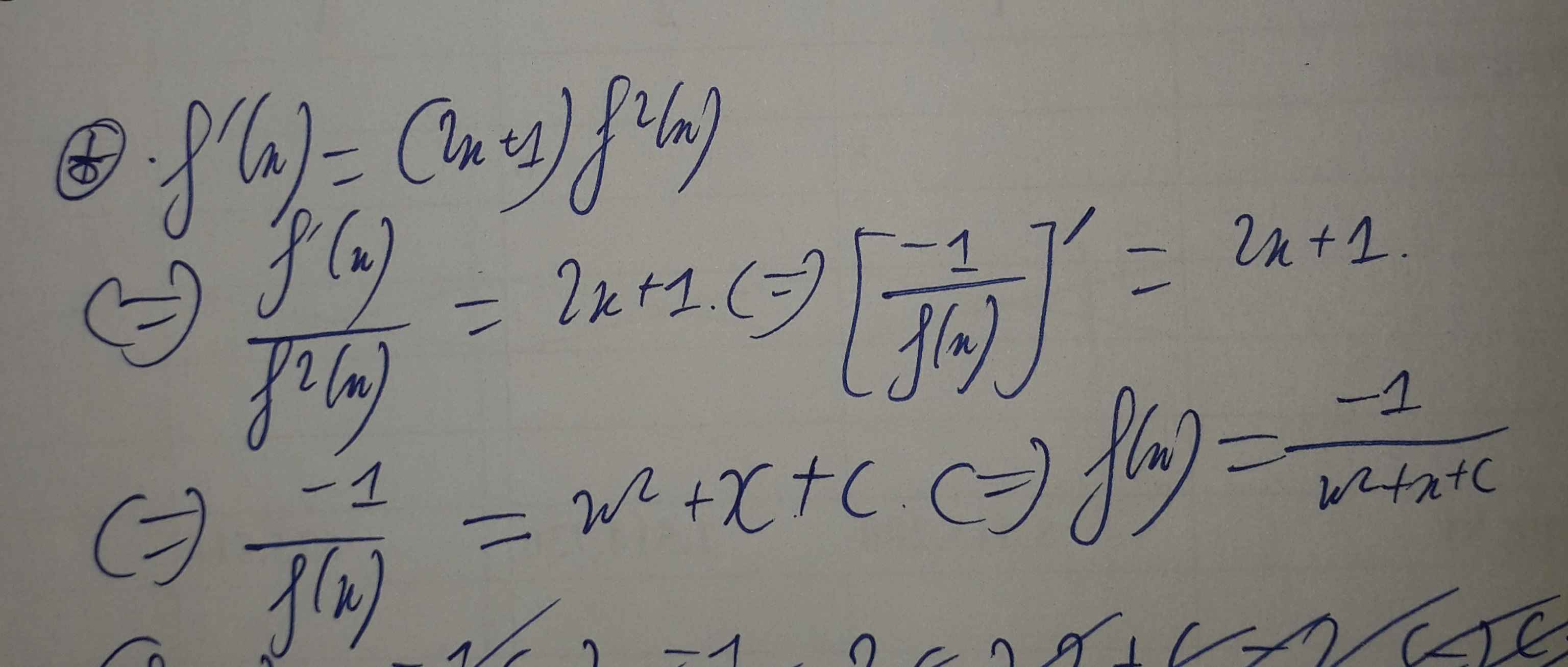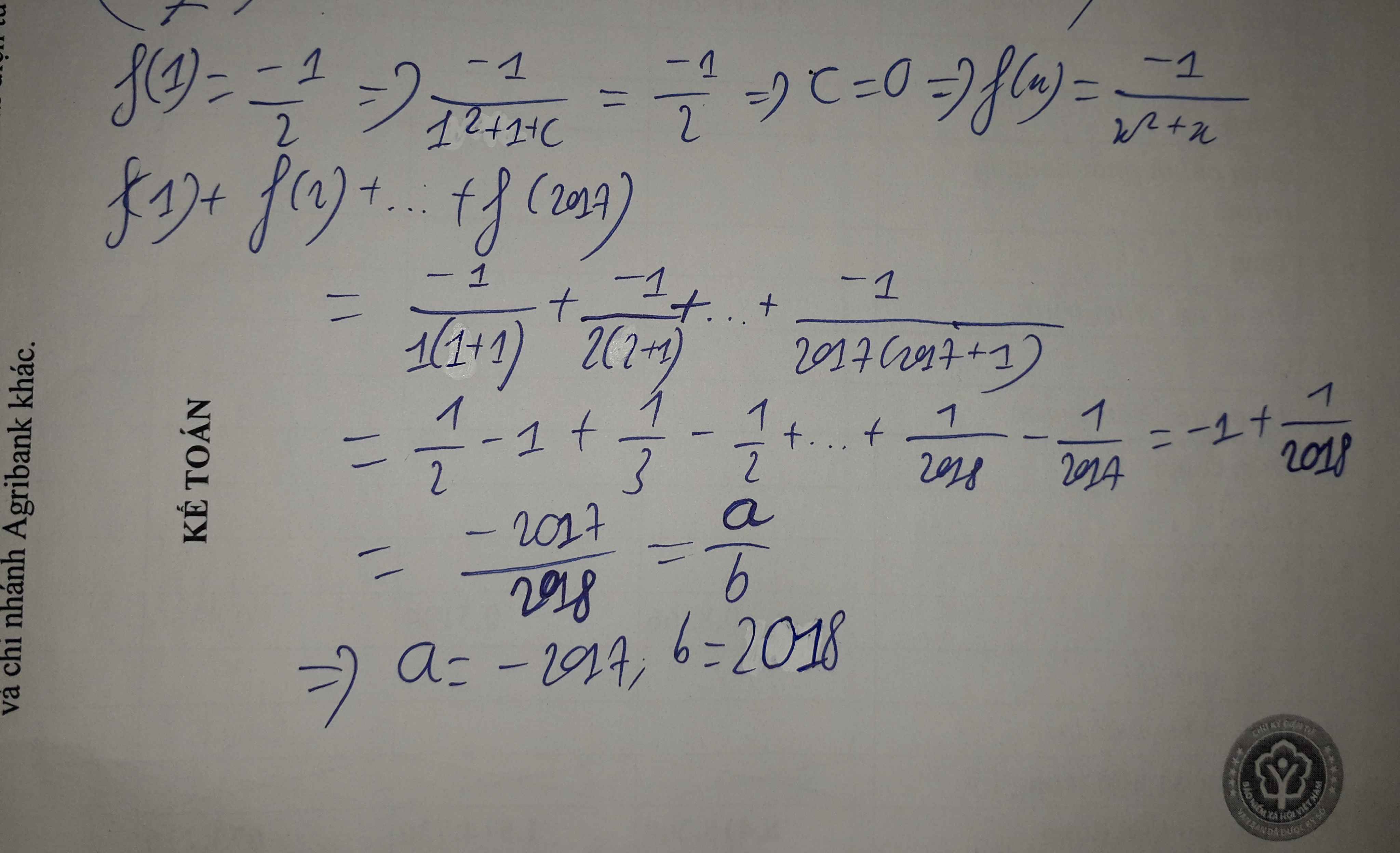Cho \(f\left(x\right)=\sin a\), trong đó \(a\ne0\). Tìm \(f^{\left(n\right)}\left(x\right)\)

Những câu hỏi liên quan
Cho đa thức \(f\left(x\right)=ax^2+bx+c\) \(\left(a\ne0\right)\). Tìm a, b, c biết \(f\left(x\right)-2020\)chia hết cho x - 1, \(f\left(x\right)+2021\) chia hết cho x + 1 và \(f\left(x\right)\) nhận giá trị bằng 2 khi x = 0
Mình có nghĩ ra cách này mọi người xem giúp mình với
f(x) = \(ax^2+bx+c\)
Ta có f(0) = 2 => c = 2
Ta đặt Q(x) = \(ax^2+bx+c-2020\)
và G(x) = \(ax^2+bx+c+2021\)
f(x) - 2020 chia cho x - 1 hay Q(x) chia cho x - 1 được số dư
\(R_1\) = Q(1) = \(a.1^2+b.1+c-2020=a+b+c-2020\)
Mà Q(x) chia hết cho x-1 nên \(R_1\) = 0
hay \(a+b+c-2020=0\). Mà c = 2 => a + b = 2018 (1)
G(x) chia cho x + 1 số dư
\(R_2\) = G(-1) = \(a.\left(-1\right)^2+b.\left(-1\right)+c+2021=a-b+2+2021\)
Mà G(x) chia hết cho x + 1 nên \(R_2\)=0
hay \(a-b+2+2021=0\) => \(a-b=-2023\) (2)
Từ (1) và (2) suy ra: \(\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}a=-\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
\(f\left(0\right)=2\Rightarrow c=2\)
\(f\left(x\right)-2020\) chia hết \(x-1\Rightarrow f\left(1\right)-2020=0\)
\(\Rightarrow a+b+c-2020=0\Rightarrow a+b-2018=0\)
\(f\left(x\right)+2021\) chia hết \(x+1\Rightarrow f\left(-1\right)+2021=0\)
\(\Rightarrow a-b+c+2021=0\Rightarrow a-b+2023=0\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=2018\\a-b=-2023\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{5}{2}\\b=\dfrac{4041}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=f\left(x\right)=ax\left(a\ne0\right)\) xác định với mọi \(x\in Q\)
Tìm giá rị của a để \(f\left(x_1\right)\cdot f\left(x_2\right)=f\left(x_1\cdot x_2\right)\)
Giúp mình với :3
\(f\left(x_1\right)=ax_1\) ; \(f\left(x_2\right)=ax_2\) ; \(f\left(x_1x_2\right)=ax_1x_2\)
Để \(f\left(x_1\right)f\left(x_2\right)=f\left(x_1x_2\right)\)
\(\Leftrightarrow ax_1.ax_2=ax_1x_2\)
\(\Leftrightarrow a^2x_1x_2=ax_1x_2\)
\(\Leftrightarrow a^2=a\)
\(\Leftrightarrow\left[{}\begin{matrix}a=0\left(loại\right)\\a=1\end{matrix}\right.\)
Vậy \(a=1\)
Đúng 2
Bình luận (0)
cho hàm số y = f(x) xác định và f(x) \(\ne0\) \(\forall x\in\left(0;+\infty\right)\), \(f'\left(x\right)=\left(2x+1\right)f^2\left(x\right)\) và f(1) = -1/2. Biết tổng f(1) + f(2) + f(3) + ... + f(2017) = a/b (a,b\(\in R\)) với a/b tối giản. Tìm a,b
Cho hàm số \(y=f\left(x\right)=\left|\sin x-\cos x\right|-\left|\sin x+\cos x\right|\) .Với mọi số nguyên dương n tính \(T=f\left(-\pi\right)+f\left(-\frac{\pi}{2}\right)+...+f\left(-\frac{\pi}{n}\right)+f\left(0\right)+f\left(\frac{\pi}{n}\right)+...+f\left(\frac{\pi}{2}\right)+f\left(\pi\right)\)
\(f\left(-x\right)=\left|-sinx-cosx\right|-\left|-sinx+cosx\right|\)
\(=\left|sinx+cosx\right|-\left|sinx-cosx\right|=-f\left(x\right)\)
\(\Rightarrow f\left(x\right)+f\left(-x\right)=0\)
\(\Rightarrow T=f\left(-\pi\right)+f\left(\pi\right)+f\left(-\frac{\pi}{2}\right)+f\left(\frac{\pi}{2}\right)+...+f\left(-\frac{\pi}{n}\right)+f\left(\frac{\pi}{n}\right)+f\left(0\right)\)
\(=0+0+...+0+f\left(0\right)=f\left(0\right)\)
\(=1-1=0\)
Đúng 0
Bình luận (0)
Cho hàm số :
\(f\left(x\right)=\left\{{}\begin{matrix}x^2\sin\dfrac{1}{x},\left(x\ne0\right)\\A,\left(x=0\right)\end{matrix}\right.\)
Xác định A để \(f\left(x\right)\) liên tục tại \(x=0\). Với giá trị A tìm được, hàm số có đạo hàm tại \(x=0\) không ?
\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).
Đúng 0
Bình luận (0)
Cho hàm số \(y=f\left(x\right)=ax+b\left(a\right);\left(a\ne0\right)\)biết đồ thị hàm số đi qua các điểm \(A\left(0;0\right);B\left(4;1\right)\)
a) tìm gía trị của a và b
b) tìm \(x\)để \(f\left(f\left(f\left(x\right)\right)\right)=-2\)
Cho hàm số f(x) = \(\left\{{}\begin{matrix}x^2sin\dfrac{1}{x}\left(x\ne0\right)\\0\left(x=0\right)\end{matrix}\right.\)
a, Tính \(g\left(x\right)=\lim\limits_{t\rightarrow0}=\dfrac{f\left(x+t\right)-f\left(x-2t\right)}{2t}\) (x thuộc R)
b, Khảo sát sự tồn tại của g'(x) với x thuộc R
cho a, f(1)=1
b,\(f\left(\frac{1}{x}\right)=\frac{1}{x^2}.f\left(x\right)\)
c,\(f\left(x_1+x_2\right)=f\left(x_1\right)+f\left(x_2\right);x_1\ne0;x_2\ne0;x_1+x_2\ne0\)
chứng minh \(f\left(\frac{5}{7}\right)=\frac{5}{7}\)
\(f\left(\frac{5}{7}\right)=f\left(\frac{1}{\frac{7}{5}}\right)=\frac{1}{\left(\frac{7}{5}\right)^2}.f\left(\frac{7}{5}\right)=\frac{25}{49}.f\left(1+\frac{2}{5}\right)=\frac{25}{49}.\left(f\left(1\right)+f\left(\frac{2}{5}\right)\right)\)
Ta có : \(f\left(\frac{2}{5}\right)=f\left(\frac{1}{5}+\frac{1}{5}\right)=f\left(\frac{1}{5}\right)+f\left(\frac{1}{5}\right)=2.f\left(\frac{1}{5}\right)=2.\frac{1}{5^2}.f\left(5\right)=\frac{2}{25}.f\left(1+1+1+1+1\right)\)
\(=\frac{2}{25}.\left(f\left(1\right)+f\left(1\right)+f\left(1\right)+f\left(1\right)+f\left(1\right)\right)=\frac{2}{25}.5=\frac{2}{5}\)
Vậy \(f\left(\frac{5}{7}\right)=\frac{49}{25}.\left(1+\frac{2}{5}\right)=\frac{25}{49}.\frac{7}{5}=\frac{5}{7}\)
Đúng 0
Bình luận (0)
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{1-\sqrt[3]{cosx}}{sin^2x}\\1\end{matrix}\right.\)khi \(^{x\ne0}_{x=0}\)
Xét tính liên tục tại \(x=0\) hay xét trên toàn miền R em nhỉ?
Đúng 0
Bình luận (2)
\(sinx=0\Rightarrow x=k\pi\)
\(\Rightarrow\) Hàm liên tục tại mọi điểm thỏa mãn \(x\ne k\pi\)
Hàm gián đoạn tại mọi điểm \(\left\{{}\begin{matrix}x=k\pi\\k\ne0\end{matrix}\right.\)
Xét tại \(x=0\):
\(\lim\limits_{x\rightarrow0}\dfrac{1-\sqrt[3]{cosx}}{sin^2x}=\lim\limits_{x\rightarrow0}\dfrac{1-cosx}{sin^2x\left(1+\sqrt[3]{cosx}+\sqrt[3]{cos^2x}\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{2sin^2\dfrac{x}{2}}{4sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}\left(1+\sqrt[3]{cosx}+\sqrt[3]{cos^2x}\right)}\)
\(=\lim\limits_{x\rightarrow0}\dfrac{1}{2cos^2\dfrac{x}{2}\left(1+\sqrt[3]{cosx}+\sqrt[3]{cos^2x}\right)}=\dfrac{1}{2.1.\left(1+1+1\right)}=\dfrac{1}{6}\ne f\left(0\right)\)
\(\Rightarrow\) Hàm gián đoạn tại \(x=0\)
Cả 4 đáp án đều sai
Đúng 0
Bình luận (0)