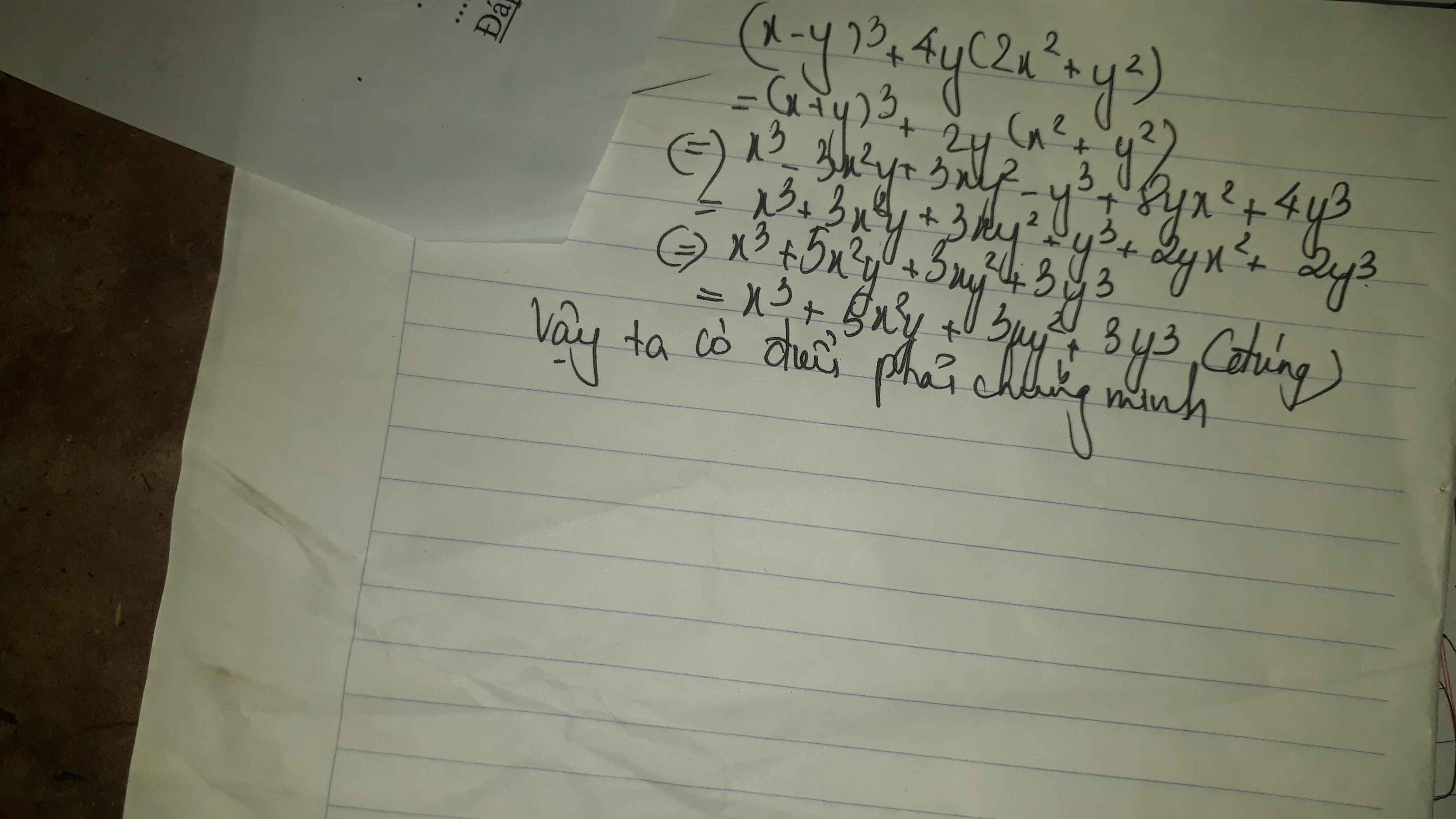Cho \(y=e^{2x}\sin5x.\). Chứng minh hệ thức \(y"-4y'+29y=0\)

Những câu hỏi liên quan
Cho y=sin^2x. Chứng minh y'''+4y=0
cho y=\(e^{sinx}\). Chứng minh hệ thức y'cosx-ysinx-y"=0
ta có y'=\(e^{sinx}.\cos sx;y"=e^{sinx}.cos^2x-sinx.e^{sinx}\)
vậy y'cosx-ysinx-y"=\(e^{sinx}.cos^2x-e^{sinx}.sinx-é^{sinx}.sinx-e^{sinx}.cos^2x+e^{sinx}.sinx=0\)
Đúng 0
Bình luận (0)
cho các biểu thức : A=11x+29y và B=2x-3y. Chứng minh rằng nếu x,y là số nguyên và A chia hết cho 13 thì B chia hết cho 13. Ngược lại nếu B chia hết cho 13 thì A chia hết cho 13
A chia hết cho 13
A+B=11x+29y+2x-3y=13x-26y chia hết cho 13
=>B chia hết cho 13
B chia hết cho 13
A+B chia hết cho 13
=>A chia hết cho 13
Đúng 1
Bình luận (0)
cho y=\(e^{-x}.\sin x.\) .chứng minh hệ thức y''+2y'+2y=0
ta có y'=\(-e^{-x}.\sin+e^{-x}.cosx\)
y"=\(e^{-x}.sinx-e^{-x}.cosx-e^{-x}.cosx-e^{-x}.sinx=-2e^{-x.cosx}\)
vậy y"+2y'+2y=\(-2e^{-x}.cosx-2e^{-x}.sinx+2e^{-x}.cosx+2e^{-x}.sinx=0\)
Đúng 0
Bình luận (0)
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
Cho đa thức :H=\(6X^3Y^4-2X^4Y^2+3X^2Y^2+5X^4Y^2-AX^3Y^4\) (A là hằng số).
a. Biết rằng bậc của đa thức bằng 6. Tìm a ?
b. Với giá trị của a vừa tìm được, chứng minh đa thức H luôn nhận giá trị dương với mọi
x khác 0; y KHÁC 0.
a: \(H=6x^3y^4-2x^4y^2+3x^2y^2+5x^4y^2-A\cdot x^3y^4\)
\(=x^3y^4\left(6-A\right)+x^4y^2\left(5-2\right)+3x^2y^2\)
\(=\left(6-A\right)\cdot x^3y^4+x^4y^2\cdot3+3x^2y^2\)
Để H có bậc là 6 thì 6-A=0
=>A=6
b: Khi A=6 thì \(H=\left(6-6\right)\cdot x^3y^4+3x^4y^2+3x^2y^2\)
\(=3x^4y^2+3x^2y^2\)
\(=3x^2y^2\left(x^2+1\right)\)
\(x^2+1>1>0\forall x\ne0\)
\(x^2>0\forall x\ne0\)
\(y^2>0\forall y\ne0\)
Do đó: \(x^2y^2\left(x^2+1\right)>0\forall x,y\ne0\)
=>\(H=3x^2y^2\left(x^2+1\right)>0\forall x,y\ne0\)
=>H luôn dương khi x,y khác 0
Đúng 0
Bình luận (0)
chứng minh đẳng thức (x-y)^3+4y(2x^2+y^2)=(x+y)^3+2y(x^2+y^2)
Ta có: \(\left(x-y\right)^3+4y\left(2x^2+y^2\right)\)
\(=x^3-3x^2y+3xy^2-y^3+8x^2y+4y^3\)
\(=x^3+5x^2y+3xy^2+3y^3\)
\(=x^3+3x^2y+3xy^2+y^3+2x^2y+2y^3\)
\(=\left(x+y\right)^3+2y\left(x^2+y^2\right)\)
Đúng 0
Bình luận (0)
Biết hpt \(\left\{{}\begin{matrix}mx-y=4\\x+my=-2\end{matrix}\right.\)luôn có 1 nghiệm (x,y)
Hệ thức liên hệ x , y mà không phụ thuộc vào m
A x2 +y2 -2x -4y =0
B x2+y2 -2x +4y =0
C x2 +y2 +2x +4y =0
D x2 + y2 + 2x - 4y =0
Mọi người giải cụ thể giúp mk ạ ... cảm ơn nhìu ạ ~~
\(\left\{{}\begin{matrix}mx-y=4\\x+my=-2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx=y+4\\my=-2-x\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}mxy=y^2+4y\left(y\ne0\right)\\mxy=-2x-x^2\left(x\ne0\right)\end{matrix}\right.\).
Suy ra \(y^2+4y=-2x-x^2\Leftrightarrow x^2+y^2+4y+2x=0\).
Đúng 0
Bình luận (0)
Chứng minh rằng không có các số x, y thỏa mãn: a) 2x² + 3x + 5 = 0 b) x² + y² - 2x - 4y + 6 = 0 c) x² + 2y² - 2xy + 2x - 6y + 10 = 0
a)\(2x^2+3x+5=0\)
\(\Leftrightarrow4x^2+6x+10=0\)
\(\Leftrightarrow\left(2x\right)^2+2.2x.\dfrac{3}{2}+\dfrac{9}{4}+\dfrac{31}{4}=0\)
\(\Leftrightarrow\left(2x+\dfrac{3}{2}\right)^2=-\dfrac{31}{4}\left(vn\right)\)
b) PT \(\Leftrightarrow\left(x^2-2x+1\right)+\left(y^2-4y+4\right)+1=0\)
\(\Leftrightarrow\left(x-1\right)^2+\left(y-2\right)^2=-1\left(vn\right)\) ( do \(VT\ge0\forall x,y\) )
c) PT \(\Leftrightarrow\left(x^2-2xy+y^2\right)+y^2+2x-6y+10=0\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1+y^2-4y+4+5=0\)
\(\Leftrightarrow\left(x-y+1\right)^2+\left(y-2\right)^2=-5\left(vn\right)\)
Vậy PT vô nghiệm
Đúng 1
Bình luận (0)
a: 2x^2+3x+5=0
=>x^2+3/2x+5/2=0
=>x^2+2*x*3/4+9/16+31/16=0
=>(x+3/4)^2+31/16=0(vô lý)
b: x^2-2x+y^2-4y+6=0
=>x^2-2x+1+y^2-4y+4+1=0
=>(x-1)^2+(y-2)^2+1=0(vô lý)
Đúng 0
Bình luận (0)