Con lắc đơn dao động điều hòa có S = 4cm, tại nơi có gia tốc trọng trường g = \(\pi^2\) m/s2. Biết chiều dài của dây là l = 1m. Hãy viết phương trình dao động biết lúc t = 0 vật đi qua vị trí cân bằng theo chiều dương.
\(S=l.\alpha_0\Rightarrow\alpha_0=\dfrac{4}{100}=0,04\left(rad\right)\)
\(\omega=\sqrt{\dfrac{g}{l}}=\pi\left(rad/s\right)\)
\(\Rightarrow\alpha=0,04\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(rad\right)\)
\(S=4\cos\left(\pi t-\dfrac{\pi}{2}\right)\left(cm\right)\)
Đúng 2
Bình luận (0)
Một con lắc đơn dài 1,0 m dao động điều hoà tại một nơi có gia tốc trọng trường do là g 9,8 m/
s
2
. Trong khi dao động, quả cầu con lắc vạch một cung tròn có độ dài 12 cm. Bỏ qua mọi ma sát. Viết phương trình dao động, biết rằng lúc đầu quả cầu con lắc đi qua vị trí cân bằng theo chiều dương.
Đọc tiếp
Một con lắc đơn dài 1,0 m dao động điều hoà tại một nơi có gia tốc trọng trường do là g = 9,8 m/ s 2 . Trong khi dao động, quả cầu con lắc vạch một cung tròn có độ dài 12 cm. Bỏ qua mọi ma sát. Viết phương trình dao động, biết rằng lúc đầu quả cầu con lắc đi qua vị trí cân bằng theo chiều dương.
x = S 0 cos φ = 0 ⇒ cos φ = 0
v = - S 0 ωsin φ > 0 ⇒ sin φ < 0
⇒ φ = - π /2
ω = 2 π /T = 2 π /2 = π rad/s
s = 6cos( π t - π /2)cm
Đúng 0
Bình luận (0)
Con lắc đơn có chiều dài l = 0,64m, dao động điều hòa tại nơi có g = 10m/s^2. Lúc t = 0, con lắc qua vị trí cân bằng theo chiều dương của quỹ đạo với vận tốc 0,4m/s. Sau 2s vận tốc con lắc là?
Ta có: \(\omega=\sqrt{\dfrac{g}{l}}=\dfrac{5\pi}{4}\left(\dfrac{rad}{s}\right)\)
\(\rightarrow A=\dfrac{v_{max}}{\omega}=\dfrac{0,4}{\dfrac{5\pi}{4}}=\dfrac{8\pi}{25}\left(m\right)\)
\(t:0\left\{{}\begin{matrix}x=0\\v>0\end{matrix}\right.\Rightarrow\varphi=-\dfrac{\pi}{2}\left(rad\right)\)
\(\rightarrow v=-4sin\left(\dfrac{5\pi}{4}t-\dfrac{\pi}{2}\right)\left(\dfrac{m}{s}\right)\)
Thay t = 2 vào \(\Rightarrow v=0\left(\dfrac{m}{s}\right)\)
Đúng 1
Bình luận (0)
Một con lắc đơn có chiều dài 1 m dao động điều hòa với chu kỳ T tại nơi có gia tốc trọng trường là g
π
2
m/
s
2
. Nhưng khi dao động khi đi qua vị trí cân bằng dây treo bị vướng đinh tại vị trí một nửa chiều dài dây treo và con lắc tiếp tục dao động. Xác định chu kỳ của con lắc đơn khi này? A. 2 s B.
2
s C.
2
+
2...
Đọc tiếp
Một con lắc đơn có chiều dài 1 m dao động điều hòa với chu kỳ T tại nơi có gia tốc trọng trường là g = π 2 m/ s 2 . Nhưng khi dao động khi đi qua vị trí cân bằng dây treo bị vướng đinh tại vị trí một nửa chiều dài dây treo và con lắc tiếp tục dao động. Xác định chu kỳ của con lắc đơn khi này?
A. 2 s
B. 2 s
C. 2 + 2 s
D. 2 + 2 2 s
Đáp án D
+ Chu kì dao động của con lắc T = π l g + π 0 , 5 l g = π 1 π 2 + π 0 , 5 π 2 = 1 + 2 2 s
Đúng 0
Bình luận (0)
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc
α
0
(rad) tại nơi có gia tốc trọng trường g (
m
/
s
2
). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là A.
v
α
0
g
l
(
m
/
s
)
B.
v...
Đọc tiếp
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc α 0 (rad) tại nơi có gia tốc trọng trường g ( m / s 2 ). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là
A. v = α 0 g l ( m / s )
B. v = α 0 g l ( m / s )
C. v = g α 0 l ( m / s )
D. v = α 0 g l ( m / s )
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc a0 (rad) tại nơi có gia tốc trọng trường g (m/s2). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là A.
v
g
α
0
l
m
/
s
B.
v
α...
Đọc tiếp
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc a0 (rad) tại nơi có gia tốc trọng trường g (m/s2). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là
A. v = g α 0 l m / s
B. v = α 0 g l m / s
C. v = α 0 g l m / s
D. v = α 0 g l m / s
Chọn đáp án D
Con lắc đơn dao động điều hòa nên ta có:
v ω A 2 − x 2 = g l α 0 2 l 2 − α 2 l 2 = g l α 0 2 − α 2 α = 0 ⇒ v = α 0 g l
Đúng 0
Bình luận (0)
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc
a
0
(rad) tại nơi có gia tốc trọng trường g (m/
s
2
). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là A. v g
α
0
l
(m/s). B. v...
Đọc tiếp
Một con lắc đơn có chiều dài l (m) dao động điều hòa với biên độ góc a 0 (rad) tại nơi có gia tốc trọng trường g (m/ s 2 ). Khi con lắc đi qua vị trí thấp nhất thì có tốc độ là
A. v = g α 0 l (m/s).
B. v = α 0 g l (m/s).
C. v = α 0 g l (m/s).
D. v = α 0 g l (m/s).
Chọn đáp án B
+ Con lắc đơn dao động điều hòa nên ta có:
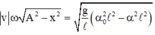
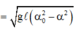
![]()
Đúng 0
Bình luận (0)
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường là g 10 m/s2. Vào thời điểm vật qua vị trí có li độ dài 8 cm thì vật có vận tốc
20
3
cm/s. Chiều dài dây treo con lắc là: A. 0,8 m. B. 1,0 m. C. 1,6 m. D. 0,2 m.
Đọc tiếp
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường là g = 10 m/s2. Vào thời điểm vật qua vị trí có li độ dài 8 cm thì vật có vận tốc 20 3 cm/s. Chiều dài dây treo con lắc là:
A. 0,8 m.
B. 1,0 m.
C. 1,6 m.
D. 0,2 m.
Từ hệ thức độc lập thời gian giữa li độ dài và vận tốc:
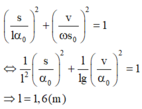
Đáp án C
Đúng 0
Bình luận (0)
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường là g 10 m/s2. Vào thời điểm vật qua vị trí có li độ dài 8 cm thì vật có vận tốc
20
3
c
m
/
s
. Chiều dài dây treo con lắc là: A. 0,8 m. B. 0,2 m. C. 1,6 m. D. 1,0 m.
Đọc tiếp
Một con lắc đơn dao động điều hòa với biên độ góc 0,1 rad ở một nơi có gia tốc trọng trường là g = 10 m/s2. Vào thời điểm vật qua vị trí có li độ dài 8 cm thì vật có vận tốc 20 3 c m / s . Chiều dài dây treo con lắc là:
A. 0,8 m.
B. 0,2 m.
C. 1,6 m.
D. 1,0 m.
Chọn đáp án C
Áp dụng công thức độc lập với hai đại lượng vuông pha là s và v:
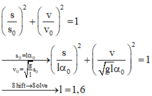
Đúng 0
Bình luận (0)
Một con lắc đơn có chiều dài l=1m, dao động điều hòa ở nơi có gia tốc trọng trường g=pi2=10m/s2. Lúc t=0, con lắc đi qua vị trí cân bằng theo chiều dương với vận tốc 0,5m/s. Sau 2,5s vạn tốc của con lắc có độ lớn là
Tần số góc của dao động con lắc đơn:
\(\omega= \sqrt{\dfrac{g}{\ell}}= \sqrt{\dfrac{\pi^2}{1}}=\pi(rad/s)\)
Biên độ: \(A=\dfrac{v_{max}}{\omega}=\dfrac{0,5}{\pi}(m/s)=\dfrac{50}{\pi}(cm/s)\)
Lúc t = 0 con lắc đi qua VTCB theo chiều dương suy ra pha ban đầu: \(\varphi=-\dfrac{\pi}{2}(rad/s)\)
Suy ra PT li độ: \(x=\dfrac{50}{\pi}\cos(\pi t-\dfrac{\pi}{2})(cm)\)
PT vận tốc: \(v=x'_{t}=-50.\sin(\pi t -\dfrac{\pi}{2})(cm/s)\)
Tại thời điểm \(t=2,5s\) vận tốc của con lắc là:
\(v=-50.\sin(\pi . 2,5 -\dfrac{\pi}{2})(cm/s)=0(cm/s)\)
Đúng 1
Bình luận (0)












