tính :
\(\int\)e2x. sin2xdx
Tính các nguyên hàm sau :
a) \(I_1=\int\sin\left(\ln x\right)dx\)
b) \(I_2=\int\left(x^2-2x+3\right)\sin2xdx\)
Tính tích phân :
\(I=\int^{\frac{\pi}{4}}_0\left(x^2-4x+3\right)\sin2xdx\)
\(I=-\frac{1}{2}\int_0^{\frac{\pi}{4}}\left(x^2-4x+3\right)d\cos2x\)
\(=-\frac{1}{2}\left[\left(x^2-4x+3\right)\cos2x\right]_0^{\frac{\pi}{4}}-\int^{^{\frac{\pi}{4}}}_0\cos2xd\left(x^2-4x+\right)\)
\(=\frac{3}{2}+\int^{^{\frac{\pi}{4}}}_0\left(x-2\right)\cos2xd=\frac{3}{2}+\frac{1}{2}\int^{^{\frac{\pi}{4}}}_0\left(x-2\right)\sin2x\)
\(=\frac{3}{2}+\frac{1}{2}\left[\left(x-2\right)\sin2x_0^{\frac{\pi}{4}}-\int^4_0\sin2dx\left(x-2\right)\right]\)
\(=\frac{3}{2}+\frac{1}{2}\left[\frac{\pi}{4}-2+\frac{1}{2}\cos2x_0^{\frac{\pi}{4}}\right]\)
\(=\frac{3}{2}+\frac{1}{2}\left[\frac{\pi}{4}-2-\frac{1}{2}\right]=\frac{\pi}{8}+\frac{1}{4}\)
1) \(\int\frac{xdx}{1+\sqrt{x-1}}\)
2) \(\int\frac{sin2xdx}{\cos^3x-\sin^2x-1}\)
3) \(\int\frac{dx}{1+\sqrt{x}+\sqrt{1+x}}\)
4) \(\int\frac{dx}{3x^3+x^2-4x}\)
5) \(\int\frac{dx}{\sqrt{9-x^2}}\)
1) Đặt \(t=1+\sqrt{x-1}\Leftrightarrow x=\left(t-1\right)^2+1\forall t\ge1\Rightarrow dx=d\left(t-1\right)^2=2dt\)
\(\Rightarrow I_1=\int\frac{\left(t-1\right)^2+1}{t}\cdot2dt=2\int\frac{t^2-2t+2}{t}dt=2\int\left(t-2+\frac{2}{t}\right)dt\\ =t^2-4t+4lnt+C\)
Thay x vào ta có...
2) \(I_2=\int\frac{2sinx\cdot cosx}{cos^3x-\left(1-cos^2x\right)-1}dx=\int\frac{-2cosx\cdot d\left(cosx\right)}{cos^3x+cos^2x-2}=\int\frac{-2t\cdot dt}{t^3+t-2}\)
\(I_2=\int\frac{-2t}{\left(t-1\right)\left(t^2+2t+2\right)}dt=-\frac{2}{5}\int\frac{dt}{t-1}+\frac{1}{5}\int\frac{2t+2}{t^2+2t+2}dt-\frac{6}{5}\int\frac{dt}{\left(t+1\right)^2+1}\)
Ta có:
\(\int\frac{2t+2}{t^2+2t+2}dt=\int\frac{d\left(t^2+2t+2\right)}{t^2+2t+2}=ln\left(t^2+2t+2\right)+C\)
\(\int\frac{dt}{\left(t+1\right)^2+1}=\int\frac{\frac{1}{cos^2m}}{tan^2m+1}dm=\int dm=m+C=arctan\left(t+1\right)+C\)
Thay x vào, ta có....
3)
\(\frac{1}{\left(1+\sqrt{x}\right)+\sqrt{x+1}}=\frac{\left(1+\sqrt{x}\right)-\sqrt{x+1}}{\left[\left(1+\sqrt{x}\right)-\sqrt{x+1}\right]\cdot\left[\left(1+\sqrt{x}\right)+\sqrt{x+1}\right]}\\ =\frac{\left(1+\sqrt{x}\right)-\sqrt{x+1}}{2\sqrt{x}}=\frac{1}{2\sqrt{x}}+\frac{1}{2}+\frac{\sqrt{x+1}}{2\sqrt{x}}\)
\(I_3=\int\left(\frac{1}{2\sqrt{x}}+\frac{1}{2}+\frac{\sqrt{x+1}}{2\sqrt{x}}\right)dx=\sqrt{x}+\frac{x}{2}+\int\sqrt{\frac{x+1}{x}}\cdot\frac{dx}{2}\)
Xét \(\int\sqrt{\frac{x+1}{x}}\cdot\frac{dx}{2}\)
Đặt \(x=tan^2t\Leftrightarrow dx=\frac{2tant}{cos^2t}\cdot dt\)
\(\Rightarrow\int\sqrt{\frac{x+1}{x}}\cdot\frac{dx}{2}=\int\sqrt{\frac{tan^2t+1}{tan^2t}}\cdot\frac{tant}{cos^2t}dt\\ =\int\frac{1}{sin^2t}\cdot\frac{sint}{cos^3t}dt=\int\frac{d\left(cost\right)}{cos^3t\left(1-cos^2t\right)}=...\)
giả sử \(I=\int\limits^{b\dfrac{\pi}{4}}_0\sin3x\sin2xdx=a+b\dfrac{\sqrt{2}}{2}\) khi đó , giá trị a+b = ?
Lời giải khác:
Áp dụng công thức:
\(\cos a-\cos b=-2\sin \frac{a+b}{2}\sin \frac{a-b}{2}\)
\(\Rightarrow \cos 5x-\cos x=-2\sin 3x\sin 2x\)
Do đó: \(I=\int ^{\frac{\pi}{4}}_{0}\sin 3x\sin 2xdx=\frac{1}{2}\int ^{\frac{\pi}{4}}_{0}(\cos x-\cos 5x)dx\)
\(=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\frac{1}{2}(\sin x-\frac{\sin 5x}{5})=\frac{3\sqrt{2}}{10}\)
Do đó : \(a=0; b=\frac{3}{5}\Rightarrow a+b=\frac{3}{5}\)
Học tại nhà - Toán - Giúp với!!!!!!!!!!!!!
giả sử \(I=\int\limits^{b\dfrac{\pi}{4}}_0\sin3x\sin2xdx=a+b\dfrac{\sqrt{2}}{2}\) khi đó , giá trị a+b = ?
a/ cho hàm số \(y=\int\left(x\right)\) = -2x+3. tính \(\int-2\) ; \(\int\left(-1\right);\int\left(0\right);\) \(\int\left(-\frac{1}{2}\right);\int\left(\frac{1}{2}\right)\)
b/ cho hàm số y=g(x)=\(x^2\)-1 . Tính g(-1); g(0); g(1); g(2)
a)
\(f\left(-2\right)=\left(-2\right).\left(-2\right)+3=4+3=7\)
\(f\left(-1\right)=\left(-2\right).\left(-1\right)+3=2+3=5\)
\(f\left(0\right)=\left(-2\right).0+3=0+3=3\)
\(f\left(-\frac{1}{2}\right)=\left(-2\right).\left(-\frac{1}{2}\right)+3=1+3=4\)
\(f\left(\frac{1}{2}\right)=\left(-2\right).\frac{1}{2}+3=\left(-1\right)+3=2\)
Câu b thì bạn cứ thế số vào và làm tương tự vậy.
chúc bạn học tốt
b)g(-1)=(-1)2-1=1-1=0
g(0)=02-1=0-1=-1
g(1)=12-1=1-1=0
g(2)=22-1=4-1=3
Tính các tích phân sau
1.I=\(\int\limits^{\frac{\Pi}{4}}_0\) (x+1)sin2xdx
2.I=\(\int\limits^2_1\frac{x^2+3x+1}{x^2+x}dx\)
3.I=\(\int\limits^2_1\frac{x^2-1}{x^2}lnxdx\)
4. I=\(\int\limits^1_0x\sqrt{2-x^2}dx\)
5.I=\(\int\limits^1_0\frac{\left(x+1\right)^2}{x^2+1}dx\)
6. I=\(\int\limits^5_1\frac{dx}{1+\sqrt{2x-1}}\)
7. I=\(\int\limits^3_1\frac{1+ln\left(x+1\right)}{x^2}dx\)
8.I=\(\int\limits^1_0\frac{x^3}{x^4+3x^2+2}dx\)
9. I=\(\int\limits^{\frac{\Pi}{4}}_0x\left(1+sin2x\right)dx\)
10. I=\(\int\limits^3_0\frac{x}{\sqrt{x+1}}dx\)
Cho I = ∫ 0 a π sin 2 x 1 + sin 2 x d x , với giá trị nguyên nào của a thì I = ∫ 0 π a sin 2 x 1 + sin 2 x d x = ln 2 ?
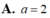
![]()
![]()
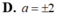
Cho I = ∫ 0 π a sin 2 x 1 + sin 2 x d x , với giá trị nguyên nào của a thì I = ∫ 0 π a sin 2 x 1 + sin 2 x d x = ln 2
A. a = 2
B. a = ± 1
C. a = -2
D. a = ± 2
Cho I = 0 π a sin 2 x 1 + sin 2 x dx , với giá trị nguyên nào của a thì I = 0 π a sin 2 x 1 + sin 2 x dx = ln 2 ?
A. a = − 2
B. a = 2
C. a = ± 1
D. a = ± 2