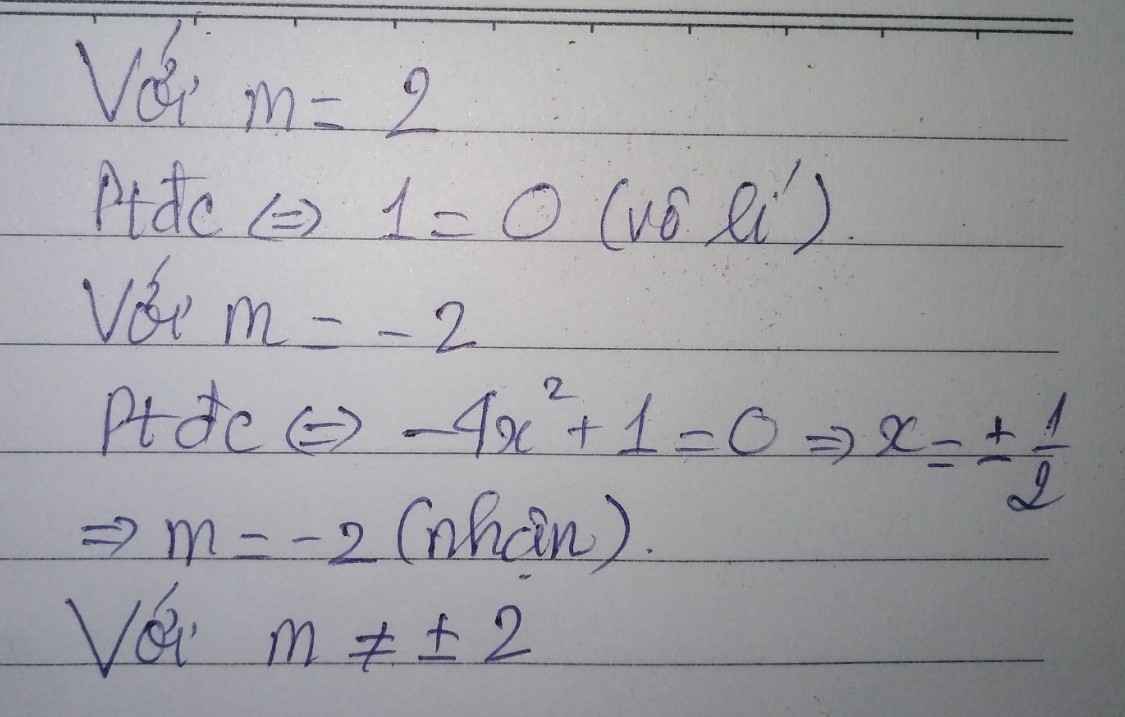giá trị của m để pt (m-4)x4-mx2+m2-4=0 có 3 mghieemj phân biệt

Những câu hỏi liên quan
Tìm tất cả giá trị của m để phương trình
x
4
-
2
(
m
+
1
)
x
2
+
m
2
-
3
0
có 4 nghiệm thực phân biệt?
A
.
(
3
;
+
∞
)
B
.
[
3...
Đọc tiếp
Tìm tất cả giá trị của m để phương trình x 4 - 2 ( m + 1 ) x 2 + m 2 - 3 = 0 có 4 nghiệm thực phân biệt?
A . ( 3 ; + ∞ )
B . [ 3 ; + ∞ )
C . ( 1 ; 6 )
D . [ 1 ; 6 )
Cho phương trình
x
4
+
m
x
2
+
2
m
+
3
0
(1). Với giá trị nào dưới đây của m thì phương trình (1) có 4 nghiệm phân biệt? A.
m
-
7
5
B. m −1 C.
m
-
3...
Đọc tiếp
Cho phương trình x 4 + m x 2 + 2 m + 3 = 0 (1). Với giá trị nào dưới đây của m thì phương trình (1) có 4 nghiệm phân biệt?
A. m = - 7 5
B. m = −1
C. m = - 3 2
D. m = 4 - 2 7
x4-mx2+m-1 =0 .Biết m= m0 là giá trị để phương trình có 4 nghiệm phân biệt trong đó hai nghiệm dương thỏa mãn |x1-x2|=1 . Tìm m0
\(x^4-1-mx^2+m=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2+1\right)-m\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x^2-1\right)\left(x^2-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=1\\x^2=m-1\end{matrix}\right.\)
Pt có 4 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\m\ne2\end{matrix}\right.\)
Khi đó ta có:
\(\left|x_1-x_2\right|=\left|1-\sqrt{m-1}\right|=1\)
\(\Leftrightarrow\left[{}\begin{matrix}1-\sqrt{m-1}=1\\1-\sqrt{m-1}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\left(loại\right)\\m=5\end{matrix}\right.\)
Vậy \(m_0=5\)
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình ( m2 - 4 ) x4 + ( m - 2 ) x 2 + 1 = 0. Có đúng hai nghiệm phân biệt.!!
Trường hợp 1: \(m\ne\pm2\)
Để phương trình có đúng hai nghiệm phân biệt thì phương trình này sẽ có hai nghiệm trái dấu
=>\(m^2-4< 0\)
hay -2<m<2
Trường hợp 2: m=2
Pt sẽ là 1=0(vô lý)
Trường hợp 3: m=-2
=>-4x2+1=0(nhận)
Vậy: -2<=m<2
Đúng 1
Bình luận (1)
Tìm tất cả các giá trị thục của m để phương trình (m2 - 4) x4 + (m - 2) x2 + 1 = 0. Có đúng hai nghiệm phân biệt.
Giúp mik gấp
Với giá trị nào của m thì mỗi PT sau có nghiệm kép ? Tìm nghiệm kép đó?
a) mx2 + 2(m + 2) x + 9 = 0 b) x2 – 2(m - 4) x+( m2 + m + 3 ) = 0
c)( m + 1) x2 – m3x + m2 ( m – 1) = 0 d) (m + 3) x2 – mx +m = 0
a: \(\Leftrightarrow\left(2m+4\right)^2-4m\cdot9=0\)
\(\Leftrightarrow4m^2+16m+16-36m=0\)
\(\Leftrightarrow m^2-5m+4=0\)
\(\Leftrightarrow\left(m-1\right)\left(m-4\right)=0\)
hay \(m\in\left\{1;4\right\}\)
b: \(\Leftrightarrow\left(2m-8\right)^2-4\left(m^2+m+3\right)=0\)
\(\Leftrightarrow4m^2-32m+64-4m^2-4m-12=0\)
=>-36m+52=0
=>-36m=-52
hay m=13/9
d: \(\Leftrightarrow m^2-4m\left(m+3\right)=0\)
\(\Leftrightarrow m\left(m-4m-12\right)=0\)
=>m(-3m-12)=0
=>m=0 hoặc m=-4
Đúng 2
Bình luận (0)
a) PT có nghiệm kép khi △=0
\(\Leftrightarrow\left[2\left(m+2\right)\right]^2-4.m.9=0\)
\(\Leftrightarrow4\left(m^2+4m+4\right)-36m=0\)
\(\Leftrightarrow4m^2-20m+16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=1\end{matrix}\right.\)
Khi đó nghiệm kép của pt là \(x_1=x_2=\dfrac{-2\left(m+2\right)}{2.m}=\dfrac{-2m-4}{2m}=-1-\dfrac{2}{m}\)
+Khi m=4 thì \(x_1=x_2=-1-\dfrac{2}{4}=-\dfrac{3}{2}\)
+Khi m=1 thì \(x_1=x_2=-1-\dfrac{2}{1}=-3\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình x 2 - m x 2 + 1 + m + 4 = 0 có bốn nghiệm phân biệt
A. m>6
B. m>4
C. m>7
D. m>5
Cho các phương trình có tham số m sau:
m
2
+
1
x
2
-
m
-
6
x
-
2
0
(1);
x
2
+
m
+
3
x
-
1
0
(2);
m
x
2
-...
Đọc tiếp
Cho các phương trình có tham số m sau:
m 2 + 1 x 2 - m - 6 x - 2 = 0 (1); x 2 + m + 3 x - 1 = 0 (2);
m x 2 - 2 x - m = 0 (3); 2 x 2 - 2 m x - 1 - m = 0 (4).
Phương trình nào có hai nghiệm phân biệt với mọi giá trị của m?
Chỉ ra khẳng định sai trong các khẳng định sau:
A. Phương trình (1)
B. Phương trình (2)
C. Phương trình (3)
D. Phương trình (4)
*Xét phương trình (m2 +1).x2 – (m- 6)x - 2= 0 có a= m2 + 1 >0 và c = -2 < 0 nên ac< 0 mọi m.
=> Phương trình (1) luôn có nghiệm mọi m.
* Phương trình x 2 + m + 3 x - 1 = 0 có ac= 1. (-1) < 0 nên phương trình này luôn có nghiệm mọi m.
* Xét (3) mx2 - 2x – m = 0 . Khi m= 0 thì (3) trở thành: - 2x = 0 đây là phương trình bậc nhất có nghiệm duy nhất là x = 0.
* Xét (4) có :
∆ = - 2 m 2 - 4 . 2 - 1 - m = 4 m 2 + 8 + 8 m = 4 m 2 + 8 m + 4 + 4 = 4 m + 1 2 + 4 > 0 ∀ m
Nên trình (4) luôn có 2 nghiệm phân biệt với mọi m.
Chọn C.
Đúng 0
Bình luận (0)
giải giùm e câu c vs ạ
c4
cho pt ẩn x: x2−2x−m2−4=0x2−2x−m2−4=0(1)
a/ giải pt đã cho khi m=1212
b/ chứng minh pt luôn có 2 nghiệm phân biệt vs mọi m
c/ tính giá trị của m để pt (1) có 2 nghiệm x1,x2 sao cho 2x1,x2(2-3x1)=2
Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ bên trái khung soạn thảo) để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (0)