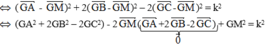cho đọan thẳng AB cố định , AB = 2a và một số k2 . Tìm tập hợp các điểm M sao cho MA2 - MB2 = k2

Những câu hỏi liên quan
Trong không gian cho ba điểm A, B, C.
Tìm tập hợp các điểm M sao cho: M A 2 + 2 M B 2 - 2 M C 2 = k 2 , với k là hằng số
Cho A(1; 2), B(-3; 1) và C(4; -2). Tìm tập hợp các điểm M sao cho MA2 + MB2= MC2
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
Đúng 0
Bình luận (0)
Cho H là một điểm cố định trên đường thẳng AB. Gọi d là đường thẳng qua H và vuông góc với AB. Lấy M di động trên d.
a. Chứng minh rằng M thay đổi thì MA2 - MB2 không đổi.
b. Lấy điểm N bất kì thỏa mãn NA2 - NB2 = HA2 - HB2. Chứng minh rằng N thuộc d
Cho tam giác ABC có AB = 22, BC = 19, CA = 13. Tìm tập hợp điểm M sao cho:
a) MA2 + MB2 + MC2 = k2b) AM2 + CM2 = BM2c) Tìm giá trị lớn nhất và giá trị nhỏ nhất của BM nếu AM2 + CM2 = BM2
a, Gọi I là trọng tâm của ΔABC
⇒ \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\)
MA2 + MB2 + MC2 = k2
⇔ 3MI2 + 2\(\overrightarrow{MI}\left(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}\right)+AB^2+AC^2+BC^2\) = k2
⇔ 3MI2 = k2 - 1014
⇔ MI = \(\sqrt{\dfrac{k-1014}{3}}\) = const
Vậy M thuộc \(\left(I;\sqrt{\dfrac{k-1014}{3}}\right)\)
Đúng 1
Bình luận (0)
Cho đoạn thẳng AB =2a , cố định .Gọi I là trung điểm của AB và k là trung điem của IB trên tia Kx tuỳ ý lấy điểm M sao cho góc kmb = góc mab tìm tập hợp điểm m
Xem chi tiết
Cho các điểm A,B cố định thỏa mãn AB = a. Tìm tập hợp M thỏa mãn \(\overrightarrow{AM}.\overrightarrow{AB}=2a^2\)
Tham khảo:
Cho 2 điểm cố định A B và AB = a. Tìm tập hợp điểm M thỏa mãn AM . AB = 2a^2
Đúng 0
Bình luận (0)
Trong không gian, cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm M sao cho MA 3MB là một măt cầu. Tìm bán kính R của măt cầu đó A. R 3 B.
R
9
2
C. R 1 D.
R
3
2
Đọc tiếp
Trong không gian, cho hai điểm A, B cố định và độ dài đoạn thẳng AB bằng 4. Biết rằng tập hợp các điểm M sao cho MA = 3MB là một măt cầu. Tìm bán kính R của măt cầu đó
A. R = 3
B. R = 9 2
C. R = 1
D. R = 3 2
Chọn D
Gọi E, F là các điểm chia trong và chia ngoài của đoạn thẳng AB theo tỉ số 3, nghĩa là

Khi đó, E , F là chân các đường phân giác trong và phân giác ngoài của góc M của tam giác MAB. Suy ra:
![]()
Vậy M thuộc mặt cầu đường kính EF. Tính được EF = 3, suy ra R=3/2
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a . Tìm tập hợp M sao cho :
2 MA2 + MB2 = MC2 + MD2
Bài 1. Cho hình chữ nhật ABCD, M là một điểm bất kì thỏa mãn AMB ̂ =900
. Chứng minh rằng MA2 + MB2 + MC2 + MD2 không đổi
Bài 2. Cho đường tròn (O,R), P là điểm cố định nằm trong đường tròn.
Qua P kẻ 2 dây cung AB và CD vuông góc với nhau.
1) Chứng minh PA2 + PB2 + PC2 + PD2 không đổi
2) Gọi M là trung điểm của AC. Chứng minh PM vuông góc với BD