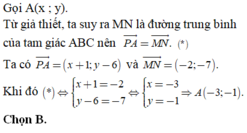Oxy cho tam giác ABC có trung điểm của BC là M(3;2). Trọng tâm và tâm đường tròn ngoại tiếp ABC lần lượt là \(G\left(\dfrac{2}{3};\dfrac{2}{3}\right)\)và\(I\left(1;-2\right)\). Xác định tọa độ đỉnh C

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC vuông tại B, BC = 2BA. Gọi E,F lần lượt là trung điểm của BC,AC. Trên tia đối của tia FE lấy điểm M sao cho FM = 3FE. Biết điểm M (5;-1), đường thẳng AC có phương trình 2x + y - 3 = 0, điểm A có hoành độ là số nguyên. Xác định tọa độ các đỉnh của tam giác ABC.
Nối BM cắt AC tại N,ta chứng minh được BM vuông góc AC và BM=AC .tìm được N,tỷ lệ AN/AC=1/5.NM/BM=3/5 => 3AN=MN.tìm đc A,có các tỷ lệ lúc nãy tìm đc B,C.
Mình tính được : A(3;-3).B(1;-3).C(1;1)
Đúng 0
Bình luận (0)
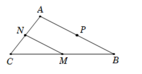
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5)
B. A(-3; -1)
C. A(-2; -7)
D. A(1; -10)
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB AC , widehat{BAC} 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( dfrac{2}{3} ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Đọc tiếp
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB = AC , \(\widehat{BAC}\) = 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( \(\dfrac{2}{3}\) ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb < 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
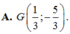
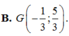
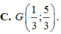
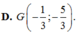
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC. A.
G
1
3
;
-
5
3
B.
G
-
1
3
;...
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tìm tọa độ trọng tâm G của tam giác ABC.
A. G 1 3 ; - 5 3
B. G - 1 3 ; 5 3
C. G 1 3 ; 5 3
D. G - 1 3 ; - 5 3
Trong mặt phẳng với hệ tọa độ Oxy cho tam giác ABC có trung điểm của cạnh BC là điểm M(3; -1), đường thẳng chứa đường co kẻ từ đỉnh B đi qua điểm E(-1;-3) và đường thẳng AC đi qua điểm F(1;3). Tìm tọa độ các đỉnh của tam giác ABC, biết rằng điểm đối xứng của đỉnh A qua tâm đường tròn ngoại tiếp tam giác ABC là điểm D(4;-2).
Trong hệ tọa độ Oxy, cho tam giác ABC có C (-2; -4), trọng tâm G(0; 4) và trung điểm cạnh BC là M (2; 0). Tổng hoành độ của điểm A và B là?
A. -2
B. 2
C. 4
D. 8
Vì M là trung điểm BC nên
x B = 2 x M − x C = 2.2 − − 2 = 6 y B = 2 y M − y C = 2.0 − − 4 = 4 ⇒ B 6 ; 4 .
Vì G là trọng tâm tam giác ABC nên
x A = 3 x G − x B − x C = − 4 y A = 3 y G − y B − y C = 12 → A − 4 ; 12 .
Suy ra x A + x B = ( − 4 ) + 6 = 2.
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.
Đúng 1
Bình luận (0)
Trong hệ trục tọa độ Oxy cho tam giác ABC có A(-1;2),B(-3;4),C(0;3). Gọi N là trung điểm của AC, M thuộc cạnh AB sao cho \(\overrightarrow{AM}=\dfrac{3}{4}\overrightarrow{AB}\). Tìm tọa độ giao điểm P của MN với BC
Đặt \(\overrightarrow{PB}=x\overrightarrow{BC}\)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=x.\overrightarrow{BC}-\dfrac{1}{3}\overrightarrow{AB}\)
\(\overrightarrow{PN}=\overrightarrow{PC}+\overrightarrow{CN}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AC}=\left(x+1\right)\overrightarrow{BC}-\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=\left(x+\dfrac{1}{2}\right)\overrightarrow{BC}-\dfrac{1}{2}\overrightarrow{AB}\)
P, M, N thẳng hàng \(\Rightarrow\dfrac{x+\dfrac{1}{2}}{x}=\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}\Rightarrow x=1\) \(\Rightarrow\overrightarrow{PB}=\overrightarrow{BC}\)
\(\Rightarrow\) B là trung điểm PC \(\Rightarrow P\left(-6;5\right)\)
Nếu bạn chưa học bài pt đường thẳng thì làm cách trên, còn học rồi thì đơn giản là thiết lập 2 pt đường thẳng BC và MN là xong
Đúng 2
Bình luận (0)