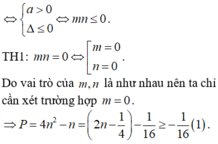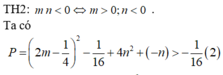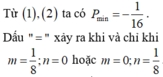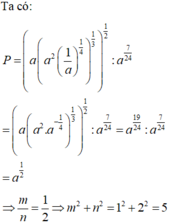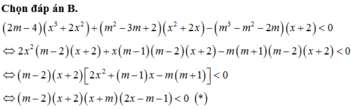cho biểu thức P = m2(m2-n)(m3-n6)(m+n2)giá trị của P khi m=16 n= -4 là...........

Những câu hỏi liên quan
tính giá trị biểu thức:
a) A=-34x + 34y biết x-y=2
b) B=ax-ay+bx-by biết a+b=-7 và x-y=-1
c)C= m2.(m2-n).(m3-n6).(m+n2) với m=-16,n=-4
a) Ta có: \(A=-34x+34y\)
\(=-34\left(x-y\right)\)
Thay x-y=2 vào biểu thức A=-34(x-y), ta được:
\(A=-34\cdot2=-68\)
Vậy: Khi x-y=2 thì A=68
b) Ta có: \(B=ax-ay+bx-by\)
\(=a\left(x-y\right)+b\left(x-y\right)\)
\(=\left(x-y\right)\left(a+b\right)\)
Thay a+b=-7 và x-y=-1 vào biểu thức \(B=\left(x-y\right)\left(a+b\right)\), ta được:
\(B=-1\cdot\left(-7\right)=7\)
Vậy: Khi a+b=-7 và x-y=-1 thì B=7
Đúng 1
Bình luận (0)
Bài 2: Tính giá trị của các biểu thức sau
a) A = 2 (m3 + n3) − 3 (m2 + n2), với m + n = 1;
b) B = 2m6 + 3m3n3 + n6 + n3, với m3 + n3 = 1;
c) C = (a − 1)3 − 4a (a + 1) (a − 1) + 3 (a − 1) (a2 + a + 1) với a = −3;
d) D = (y − 1) (y − 2) (1 + y + y2) (4 + 2y + y2) với y = 1
a: \(A=2\left(m^3+n^3\right)-3\left(m^2+n^2\right)\)
\(=2\left[\left(m+n\right)^3-3mn\left(m+n\right)\right]-3\left[\left(m+n\right)^2-2mn\right]\)
\(=2-6mn-3+6mn\)
=-1
c: \(C=\left(a-1\right)^3-4a\left(a+1\right)\left(a-1\right)+3\left(a-1\right)\left(a^2+a+1\right)\)
\(=a^3-3a^2+3a-1-4a\left(a^2-1\right)+3a^3-3\)
\(=4a^3-3a^2+3a-4-4a^3+4a\)
\(=-3a^2+7a-4\)
\(=-3\cdot9-21-4\)
=-27-21-4
=-52
Đúng 0
Bình luận (0)
Cho biểu thức:
P =( m 2 -2m + 4)(m + 2)- m 3 +(m + 3)(m -3)- m 2 -18.
Chứng minh giá trị của P không phụ thuộc vào m.
Hàm số
y
(
x
+
m
)
3
+
(
x
+
n
)
3
-
x
3
đồng biến trên khoảng
(...
Đọc tiếp
Hàm số y = ( x + m ) 3 + ( x + n ) 3 - x 3 đồng biến trên khoảng ( - ∞ ; + ∞ ) . Giá trị nhỏ nhất của biểu thức P = 4 ( m 2 + n 2 ) - m - n bằng
A. - 16
B. 4
C. - 1 16
D. 1 4
Các thầy cô giúp dùm em với ạ
Cho 2 số không âm x, y thỏa mãn x2 + y2 x+y+xy. Biết rằng tập giá trị của biểu thức S x+ y là [m ; n]. Tính giá trị của biểu thức m2+n2
A. 16. B. 13 C. 25 D. 34
Đọc tiếp
Các thầy cô giúp dùm em với ạ
Cho 2 số không âm x, y thỏa mãn x2 + y2 = x+y+xy. Biết rằng tập giá trị của biểu thức S = x+ y là [m ; n]. Tính giá trị của biểu thức m2+n2
A. 16. B. 13 C. 25 D. 34
Ta có \(xy\le\dfrac{\left(x+y\right)^2}{4}\).
Do đó ta có: \(x+y+xy=x+y-2xy+3xy\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Rightarrow x^2+y^2\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Leftrightarrow\dfrac{1}{4}\left(x+y\right)^2-\left(x+y\right)\le0\)
\(\Leftrightarrow\left(x+y\right)\left[\dfrac{1}{4}\left(x+y\right)-1\right]\le0\)
\(\Leftrightarrow0\le x+y\le4\).
Do đó m = 0, n = 4.
Vậy m2 + n2 = 16. Chọn A.
Đúng 4
Bình luận (1)
Rút gọn biểu thức
P
a
a
2
1
a
1
4
1...
Đọc tiếp
Rút gọn biểu thức P = a a 2 1 a 1 4 1 3 1 2 : a 7 24 ta được biểu thức dạng a m n , trong đó m n là phân số tối giản, m , n ∈ ℕ * . Tính giá trị m 2 + n 2
A. 5
B. 13
C. 10
D. 25
Rút gọn biểu thức
P
a
a
2
1
a
1
4
1...
Đọc tiếp
Rút gọn biểu thức P = a a 2 1 a 1 4 1 3 1 2 : a 7 24 ta được biểu thức dạng a m n , trong đó m n là phân số tối giản, m , n ∈ ℕ * . Tính giá trị m 2 + n 2
A. 5
B. 13
C. 10
D. 25
Tính giá trị của biểu thứca) M
x
2
- 8x + 7 tại x 49;b) N
x
4
- 2
x
3
+
x
2
tại x 10;c) P
m
6
-
2
m
4
- m +
m
2
+
m...
Đọc tiếp
Tính giá trị của biểu thức
a) M = x 2 - 8x + 7 tại x = 49;
b) N = x 4 - 2 x 3 + x 2 tại x = 10;
c) P = m 6 - 2 m 4 - m + m 2 + m 3 biết m 3 - m + 2 = 0.
Đồ thị hàm số y=x2 đi qua hai điểm (\(\sqrt{2}\);m)và(-\(\sqrt{3}\);n).Khi đó giá trị của biểu thức m2-n2 bằng
A.5 B.-1 C.1 D.-5
Thay hai điểm `(\sqrt{2};m)` và `(-\sqrt{3};n)` vào `y=x^2` ta có:
`{(m=(\sqrt{2})^2),(n=(-\sqrt{3})^2):}<=>{(m^2=4),(n^2=9):}`
`=>m^2-n^2=4-9=-5`
`->bb D`
Đúng 2
Bình luận (0)
Thay hai điểm vào hàm số
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{2}=m^2\\-\sqrt{3}=n^2\end{matrix}\right.\)
\(m^2-n^2=\sqrt{2}-\left(-\sqrt{3}\right)=\sqrt{2}+\sqrt{3}\)
Đúng 0
Bình luận (0)
Gọi n là số các giá trị của tham số m để bất phương trình
(
2
m
-
4
)
(
x
3
+
2
x
2
)
+
(
m
2
-
3
m
+
2
)
-
(
m
3
–
m
2
-
2
m...
Đọc tiếp
Gọi n là số các giá trị của tham số m để bất phương trình ( 2 m - 4 ) ( x 3 + 2 x 2 ) + ( m 2 - 3 m + 2 ) - ( m 3 – m 2 - 2 m ) ( x + 2 ) < 0 vô nghiệm. Giá trị của n bằng
A. 5
B. 1
C. 4
D. 2