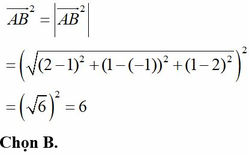Trong không gian \(Oxyz\), cho điểm \(A\left(-1;2;1\right)\) .Mặt phẳng qua \(A\) và vuông góc với trục \(Ox\) là:

Những câu hỏi liên quan
Trong không gian Oxyz, cho điểm A(1;−2;3). Điểm đối xứng với điểm A qua mặt phẳng (Oxyz) là
A. (−1;2;−3)
B. (1;2;3)
C. (−1;2;−3)
D. (1;−2;−3)
Trong không gian Oxyz, cho 3 điểm \(A=\left(1;-1;1\right);B=\left(0;1;2\right);C=\left(1;0;1\right)\). Tìm tọa độ trọng tâm G của tam giác ABC ?
Trong không gian Oxyz, cho đường thẳng d:dfrac{x-1}{2}dfrac{y-2}{2}dfrac{z}{1} và hai điểm Aleft(1;-1;1right), Bleft(4;2;-2right). Gọi Δ là đường thẳng đi qua A và vuông góc với d sao cho khoảng cách từ điểm B đến Δ là nhỏ nhất. Phương trình đường thẳng Δ là:A. dfrac{x-1}{-1}dfrac{y+1}{1}dfrac{z-1}{4} B. dfrac{x-1}{1}dfrac{y+1}{1}dfrac{z-1}{4}C. dfrac{x-1}{1}dfrac{y+1}{-1}dfrac{z-1}{4} D. dfrac{x-1}{1}dfrac{y+1}{1}dfrac{z-1}{-4}
Đọc tiếp
Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{x-1}{2}=\dfrac{y-2}{2}=\dfrac{z}{1}\) và hai điểm \(A\left(1;-1;1\right)\), \(B\left(4;2;-2\right)\). Gọi Δ là đường thẳng đi qua \(A\) và vuông góc với \(d\) sao cho khoảng cách từ điểm \(B\) đến Δ là nhỏ nhất. Phương trình đường thẳng Δ là:
A. \(\dfrac{x-1}{-1}=\dfrac{y+1}{1}=\dfrac{z-1}{4}\) B. \(\dfrac{x-1}{1}=\dfrac{y+1}{1}=\dfrac{z-1}{4}\)
C. \(\dfrac{x-1}{1}=\dfrac{y+1}{-1}=\dfrac{z-1}{4}\) D. \(\dfrac{x-1}{1}=\dfrac{y+1}{1}=\dfrac{z-1}{-4}\)

Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng
Đúng 1
Bình luận (4)
Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều 3 điểm \(A\left(1;1;1\right);B\left(-1;1;0\right);C\left(3;1;-1\right)\) ?
Trong không gian tọa độ Oxyz cho đường thẳng d:dfrac{x-1}{2}dfrac{y-1}{2}dfrac{z+1}{1} và hai điểm Aleft(6;0;0right), Bleft(0;0;-6right). Khi điểm M thay đổi trên đường thẳng d, hãy tìm giá trị nhỏ nhất của biểu thức PMA+MBA. minP6sqrt{3} B. minP6sqrt{2} C. minP9 D. minP12Mình cần bài giải ạ, mình cảm ơn nhiều♥
Đọc tiếp
Trong không gian tọa độ \(Oxyz\) cho đường thẳng \(d:\dfrac{x-1}{2}=\dfrac{y-1}{2}=\dfrac{z+1}{1}\) và hai điểm \(A\left(6;0;0\right)\), \(B\left(0;0;-6\right)\). Khi điểm \(M\) thay đổi trên đường thẳng \(d\), hãy tìm giá trị nhỏ nhất của biểu thức \(P=MA+MB\)
A. \(minP=6\sqrt{3}\) B. \(minP=6\sqrt{2}\) C. \(minP=9\) D. \(minP=12\)
Mình cần bài giải ạ, mình cảm ơn nhiều♥

Phương trình d dạng tham số: \(\left\{{}\begin{matrix}x=1+2t\\y=1+2t\\z=-1+t\end{matrix}\right.\)
Gọi \(M\left(1+2t;1+2t;-1+t\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(2t-5;2t+1;t-1\right)\\\overrightarrow{BM}=\left(2t+1;2t+1;t+5\right)\end{matrix}\right.\)
\(\Rightarrow P=\sqrt{\left(2t-5\right)^2+\left(2t+1\right)^2+\left(t-1\right)^2}+\sqrt{\left(2t+1\right)^2+\left(2t+1\right)^2+\left(t+5\right)^2}\)
\(=\sqrt{9t^2-18t+27}+\sqrt{9t^2+18t+27}\)
\(=\sqrt{\left(3-3t\right)^2+18}+\sqrt{\left(3+3t\right)^2+18}\)
\(\ge\sqrt{\left(3-3t+3+3t\right)^2+4.18}=6\sqrt{3}\)
Đúng 2
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng Delta_m:left{{}begin{matrix}x1-m+left(m-1right)ty3-m+left(m+1right)tzm-mtend{matrix}right. với m là tham số và điểm Aleft(5;3;1right). Viết phương trình đường thẳng Delta_m, biết rằng dleft(A;Delta_mright) nhỏ nhất.A.left{{}begin{matrix}x4ty4-2tz-tend{matrix}right.B.left{{}begin{matrix}x5+4ty3-2tz2-tend{matrix}right.C.left{{}begin{matrix}x4ty4+6tz-tend{matrix}right.D.left{{}begin{matrix}x5+ty3+tz2+2tend{matrix}right.
Đọc tiếp
Trong không gian với hệ toạ độ \(Oxyz\), cho đường thẳng \(\Delta_m:\left\{{}\begin{matrix}x=1-m+\left(m-1\right)t\\y=3-m+\left(m+1\right)t\\z=m-mt\end{matrix}\right.\) với \(m\) là tham số và điểm \(A\left(5;3;1\right)\). Viết phương trình đường thẳng \(\Delta_m\), biết rằng \(d\left(A;\Delta_m\right)\) nhỏ nhất.
\(A.\left\{{}\begin{matrix}x=4t\\y=4-2t\\z=-t\end{matrix}\right.\)
\(B.\left\{{}\begin{matrix}x=5+4t\\y=3-2t\\z=2-t\end{matrix}\right.\)
\(C.\left\{{}\begin{matrix}x=4t\\y=4+6t\\z=-t\end{matrix}\right.\)
\(D.\left\{{}\begin{matrix}x=5+t\\y=3+t\\z=2+2t\end{matrix}\right.\)
Để tìm phương trình đường thẳng Δm, ta thay các giá trị của x, y, z vào phương trình của Δm:
x = 1 - m + (m - 1)t
y = 3 - m + (m + 1)t
z = m - mt
Thay A(5, 3, 1) vào phương trình của Δm:
5 = 1 - m + (m - 1)t
3 = 3 - m + (m + 1)t
1 = m - mt
Từ đó, ta có hệ phương trình:
4 = (m - 1)t
0 = 2t
-4 = 2mt
Giải hệ phương trình này, ta được t = 0 và m = 1.
Thay t = 0 và m = 1 vào phương trình của Δm, ta có:
x = 1 - 1 + (1 - 1) * 0 = 0
y = 3 - 1 + (1 + 1) * 0 = 2
z = 1 - 1 * 0 = 1
Vậy phương trình đường thẳng Δm là:
x = 0
y = 2
z = 1
Do đó, đáp án là A.
Đúng 1
Bình luận (1)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu left(Sright):left(x+1right)^2+left(y-2right)^2+left(z-3right)^248 và đường thẳng left(dright):dfrac{x+1}{1}dfrac{y-2}{1}dfrac{z-3}{sqrt{2}} . Điểm Mleft(a;b;cright)left(a0right) nằm trên đường thẳng left(dright) sao cho từ M kẻ được 3 tiếp tuyến MA,MB,MC đến mặt cầu left(Sright) thỏa mãn widehat{AMB}60^o,widehat{BMC}90^o,widehat{CMA}120^o. Tính Qa+b-c?
Đọc tiếp
Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt cầu \(\left(S\right):\left(x+1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=48\) và đường thẳng \(\left(d\right):\dfrac{x+1}{1}=\dfrac{y-2}{1}=\dfrac{z-3}{\sqrt{2}}\) . Điểm \(M\left(a;b;c\right)\left(a>0\right)\) nằm trên đường thẳng \(\left(d\right)\) sao cho từ \(M\) kẻ được 3 tiếp tuyến \(MA,MB,MC\) đến mặt cầu \(\left(S\right)\) thỏa mãn \(\widehat{AMB}=60^o,\widehat{BMC}=90^o,\widehat{CMA}=120^o\). Tính \(Q=a+b-c\)?
Trong không gian Oxyz, cho hai điểm A(1;-1;2) và B(2;1;1). Tính →AB2
A. 2
B. 6
C. 3
D. 4
Trong không gian Oxyz, cho điểm A(1;-2;4) Hình chiếu vuông góc của A trên trục Oy là điểm
A. (0;0;4)
B. (1;0;0)
C. (0;-2;0)
D. (0;-2;4)