Trục Ox nhận \(\left(1;0;0\right)\) là 1 vtcp
Do đó mặt phẳng vuông góc Ox nhận \(\left(1;0;0\right)\) là 1 vtpt
Phương trình:
\(1\left(x+1\right)+0\left(y-2\right)+0\left(z-1\right)=0\)
\(\Leftrightarrow x+1=0\)
Trục Ox nhận \(\left(1;0;0\right)\) là 1 vtcp
Do đó mặt phẳng vuông góc Ox nhận \(\left(1;0;0\right)\) là 1 vtpt
Phương trình:
\(1\left(x+1\right)+0\left(y-2\right)+0\left(z-1\right)=0\)
\(\Leftrightarrow x+1=0\)
Trong không gian Oxyz, đường thẳng đi qua điểm A(-1;2;1) và vuông góc với mặt phẳng (P):x-2y-z-5=0 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;2;1) và B(3;1;0). Mặt phẳng (P) song song với đường thẳng AB và trục Ox có một véc tơ pháp tuyến là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng d đi qua điểm A(1;2;1) và vuông góc với mặt phẳng (P): x-2y+z-1=0 có dạng
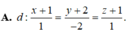
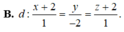
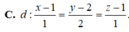
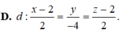
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(0;1;2), B(2;-2;1), C(-2;0;1). Phương trình mặt phẳng đi qua A và vuông góc với BC là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho 2 điểm A(0;3;0), B(0;0;-4) và (P): x+2z=0. Gọi C thuộc trục Ox sao cho mặt phẳng (ABC) vuông góc với mặt phẳng (P). Tọa độ tâm mặt cầu ngoại tiếp tứ diện OABC là
A. ( 1 ; 3 2 ; - 2 )
B. ( - 1 ; - 3 2 ; 2 )
C. ( 1 2 ; 3 2 ; - 1 )
D. ( 1 ; 0 ; - 2 )
Trong không gian với hệ tọa độ Oxyz, xét đường thẳng Δ đi qua điểm A (0;0;1) và vuông góc với mặt phẳng Ozx. Tính khoảng cách nhỏ nhất giữa điểm B (0; 4; 0) tới điểm C trong đó C là điểm cách đều đường thẳng Δ và trục Ox
A. 1/2
B. 3 2
C. 6
D. 65 / 2
Trong không gian (Oxyz), cho mặt phẳng (P) đi qua hai điểm A(5;-1;1), B(3;1;-1) và song song với trục Ox, Phương trình của mặt phẳng (P) là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của A lên các trục Ox, Oy, Oz. Phương trình của mặt phẳng A 1 A 2 A 3 là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng (P) đi qua hai điểm A(0;1;0), B(2;3;1) và vuông góc với mặt phẳng (Q):x+2y-z=0 có phương trình là
![]()
![]()
![]()
![]()