Cho tam giác ABC vuông tại A, AH vuông góc với BC (H thuộc BC). Chứng minh góc C=góc BAH

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Các tia phân giác của góc C và góc BAH cắt nhau tại K. Chứng minh Ak vuông góc với CK?
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc BC (H thuộc BC). Tia phân giác góc BAH và góc C cắt nhau tại K .Chứng minh AK vuông góc CK
cho tam giác abc cân tại a có AB=AC=5cm, BC=8cm. kẻ AH vuông góc với BC (H thuộc BC) a) chứng minh HB=HC và góc BAH= góc CAH. b) tính độ dài AH. c) kẻ HD vươong góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
b: BH=CH=BC/2=4(cm)
nên AH=3(cm)
c: Xét ΔAEH vuông tại E và ΔADH vuông tại D có
AH chung
\(\widehat{EAH}=\widehat{DAH}\)
DO đó: ΔAEH=ΔADH
Suy ra: HE=HD
hay ΔHDE cân tại H
Đúng 3
Bình luận (1)
Câu 8 Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H BC) a) Chứng minh HB HC b) Chứng minh góc BAH góc CAH c) Kẻ HD vuông góc với AB (D thuộc AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân
Đọc tiếp
Câu 8 Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H ![]() BC)
BC)
a) Chứng minh HB = HC
b) Chứng minh góc BAH =góc CAH
c) Kẻ HD vuông góc với AB (D thuộc AB). Kẻ HE vuông góc với AC (E ![]() AC). Chứng minh tam giác HDE là tam giác cân
AC). Chứng minh tam giác HDE là tam giác cân
a: Ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
hay HB=HC
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
hay \(\widehat{BAH}=\widehat{CAH}\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: HD=HE
hay ΔHDE cân tại H
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc với BC ( H thuộc BC )
a) Chứng minh: HB = HC và góc BAH = góc CAH
c) Kẻ HD vuông góc với AB tại D, HE vuông góc với AC tại E. Chứng minh tam giác HDE cân.
Cho tam giác ABC cân tại A ,kẻ AH vuông góc với BC ( H thuộc BC )
a) Chứng minh góc BAH = góc ACH
b) Cho AH = 3cm , BC = 8cm . Tính độ dài của cạnh AC
c) Kẻ HE vuông góc với AB , HD vuông góc với AC . Chứng minh AE = AD
d) Chứng ming ED song song với BC
Giúp mình vs lm ơn , đang lm bt tết nên cần gấp ạ , xin chân thành cảm ơn :3
đề bài có lỗi ko bạn ?
a, Vì tam giác ABC cân tại A
AH là đường cao nên đồng thời là đường phân giác
=> ^BAH = ^CAH
b, Vì tam giác ABC cân tại A nên AH đồng thời là đường trung tuyến
=> HB = HC = BC/2 = 4 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=\sqrt{9+16}=5cm\)
c, Xét tam giác AEH và tam giác ADH ta có :
^EAH = ^DAH (cmt)
AH_chung
^AEH = ^ADH = 900
Vậy tam giác AEH = tam giác ADH ( ch - gn )
=> AE = AD ( 2 cạnh tương ứng )
d, Ta có : \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)vì AE = AD ; AB = AC
=> ED // BC
Đúng 4
Bình luận (1)
cho tam giác ABC vuông tại A. vẽ AH vuông góc với BC tại H. Chứng minh rằng góc BAH= góc C
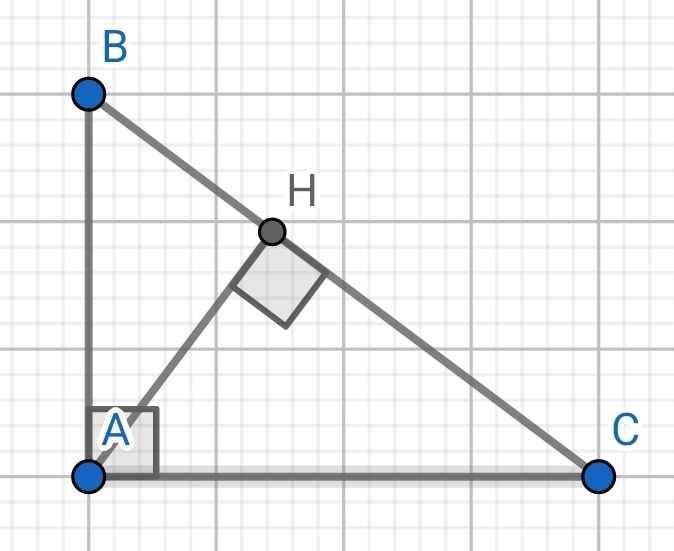
∆AHB vuông tại H
⇒∠BAH + ∠ABH = ∠BAH + ∠ABC = 90⁰ (1)
∆ABC vuông tại A
⇒ ∠ABC + ∠ACB = 90⁰ (2)
Từ (1) và (2) ⇒ ∠BAH = ∠ACB
Hay ∠BAH = ∠C
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại A .kẻ AH vuông góc với BC( H thuộc BC).các tia phân giác của các góc BAH và ACB cắt nhau tại K ,chứng minh AK vuông góc với CK
Bạn tham khảo ở đây nhé:
Câu hỏi của ngô thị gia linh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Đường cao AH (H thuộc BC).
a) Chứng minh H là trung điểm của BC và góc BAH = góc HAC.
b) Kẻ HM vuông góc với AB tại M và HN vuông góc với AC tại N. Chứng minh tam giác AMN cân tại A.
c) Vẽ P sao cho H là trung điểm đoạn NP. Chứng minh AH, MN, DP đồng quy.
d) MP cắt BC tại K, NK cắt MH tại D. Chứng minh AH, MN, DP đồng quy.
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
=>HB=HC và góc BAH=góc CAH
b: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
góc MAH=góc NAH
=>ΔAMH=ΔANH
=>AM=AN
=>ΔAMN cân tại A
Đúng 1
Bình luận (0)
















