Giúp mình bài số 4 với ạ,cảm ơn

Những câu hỏi liên quan
giúp mình bài 4 với ạ mình cảm ơn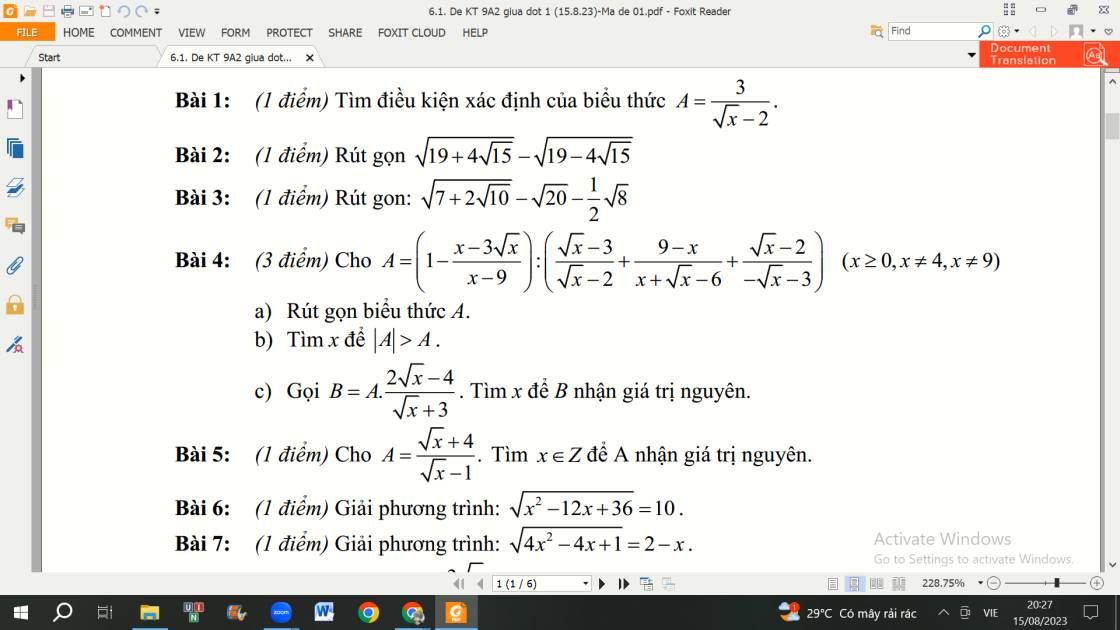
4:
a: \(A=\left(\dfrac{x-9-x+3\sqrt{x}}{x-9}\right):\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{x-9+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{x-9}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{-3}{\sqrt{x}-2}\)
b: |A|>A
=>A<0
=>\(\dfrac{-3}{\sqrt{x}-2}< 0\)
=>căn x-2>0
=>x>4
c: \(B=\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\cdot\dfrac{-3}{\left(\sqrt{x}-2\right)}=\dfrac{-6}{\sqrt{x}+3}\)
Để B là số nguyên thì \(\sqrt{x}+3\inƯ\left(-6\right)\)
=>\(\sqrt{x}+3\in\left\{3;6\right\}\)
=>\(x\in\left\{0;9\right\}\)
mà x<>9
nên x=0
Đúng 1
Bình luận (0)
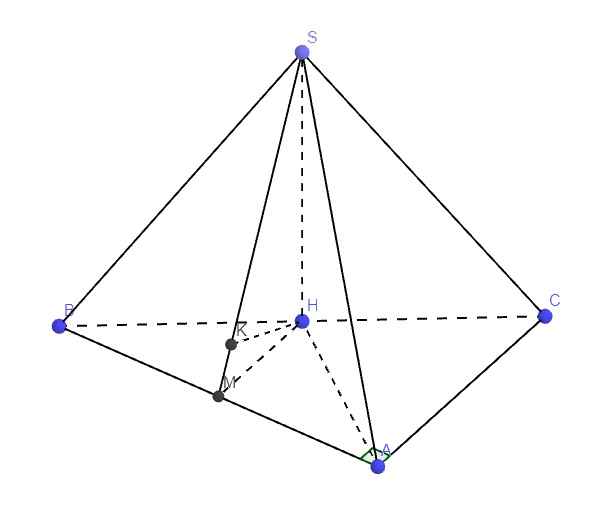
Giúp mình bài 4 với ạ mình cảm ơn
a.
\(SH\perp\left(ABC\right)\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\Rightarrow\Delta SBH\) vuông tại H
\(BH=\dfrac{1}{2}BC=a\Rightarrow SH=\sqrt{SB^2-BH^2}=a\sqrt{3}\)
\(SH\perp\left(ABC\right)\Rightarrow HA\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(AH=\dfrac{1}{2}BC=a\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SAH}=\dfrac{SH}{AH}=\sqrt{3}\Rightarrow\widehat{SAH}=60^0\)
b.
H là trung điểm BC, M là trung điểm AB \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH||AC\Rightarrow MH\perp AB\) (do \(AB\perp AC\))
Lại có \(SH\perp\left(ABC\right)\Rightarrow SH\perp AB\)
\(\Rightarrow AB\perp\left(SMH\right)\)
Mà \(AB=\left(SAB\right)\cap\left(ABC\right)\Rightarrow\widehat{SMH}\) là góc giữa (SAB) và (ABC)
\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\) \(\Rightarrow MH=\dfrac{1}{2}AC=\dfrac{a\sqrt{3}}{2}\) (đường trung bình)
\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{MH}=2\Rightarrow\widehat{SMH}\approx63^023'\)
c.
Theo cmt: \(\left\{{}\begin{matrix}MH\perp SH\\MH\perp AB\end{matrix}\right.\) \(\Rightarrow MH\) là đường vuông góc chung của SH và AB
\(\Rightarrow d\left(SH;AB\right)=MH=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ HK vuông góc SM (K thuộc SM)
\(AB\perp\left(SMH\right)\Rightarrow AB\perp HK\)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
Hệ thức lượng trong tam giác vuông SMH:
\(HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{a\sqrt{15}}{5}\)
Đúng 0
Bình luận (0)
giúp mình bài 4 với ạ! mk cảm ơn ạ!
Mọi người giải giúp mình bài 4 với ạ mình cảm ơn
a, Xét tam giác ABC vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=\dfrac{81}{4}+36=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\dfrac{81}{4}}{\dfrac{15}{2}}=\dfrac{27}{10}\)cm
=> \(CH=BC-BH=\dfrac{15}{2}-\dfrac{27}{10}=\dfrac{24}{5}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}\)
\(=\dfrac{4,5.6}{\dfrac{15}{2}}=\dfrac{18}{5}\)cm
Đúng 3
Bình luận (0)
tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow BC^2=AB^2+AC^2=\left(4,5\right)^2+6^2=\dfrac{225}{4}\Rightarrow BC=\dfrac{15}{2}=7,5\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{\left(4,5\right)^2}{7,5}=\dfrac{27}{10}=2,7\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{6^2}{7,5}=\dfrac{24}{5}=4,8\left(cm\right)\)
Đúng 2
Bình luận (2)
 Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
Đúng 1
Bình luận (1)
Mn giúp mình giải bài 3 và 4 với ạ mình cảm ơn mn mong mn giúp 🥺
Bây h dùng pm hoidap247 rùi nhé
Nhiều ngưòi on lắm
Mình nghĩ là bài 4, câu a là 6 học sinh chỉ giỏi môn Tiếng Anh.
Còn câu b thì là lớp 9A có 62.
Mình nghĩ vậy thôi chứ chưa chắc đúng. Bài toán khó quá, mình cũng ko bit mình nói đúng hay sai nữa.
Mn giúp mình với ạ!Mình cảm ơn!!!
Bài 1:Chứng minh rằng B = 2 + 22 + 23 + 24 + ........ + 299 + 2100 chia hết cho 31.
Mình cảm ơn mn ạ!Giúp mình với tối nay 20:00 mình phải nộp bài rồi!!!
![]()
\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
Đúng 5
Bình luận (1)
B=2+22+23+24+...+299+2100=2(1+22+23+24)+...+296(1+22+23+24)=2.31+26.31+...+296.31=31(2+26+...+296)⋮31
Đúng 1
Bình luận (0)