 Giải giúp bài d
Giải giúp bài d
các bạn ơi giải giúp mình với, cảm ơn nhìu(có thể giải 1 trong 2 bài nhưng đủ các ý trong bài đó giúp mình :D)
Giúp mik giải bài 4 vs câu d bài 2 zứi. :^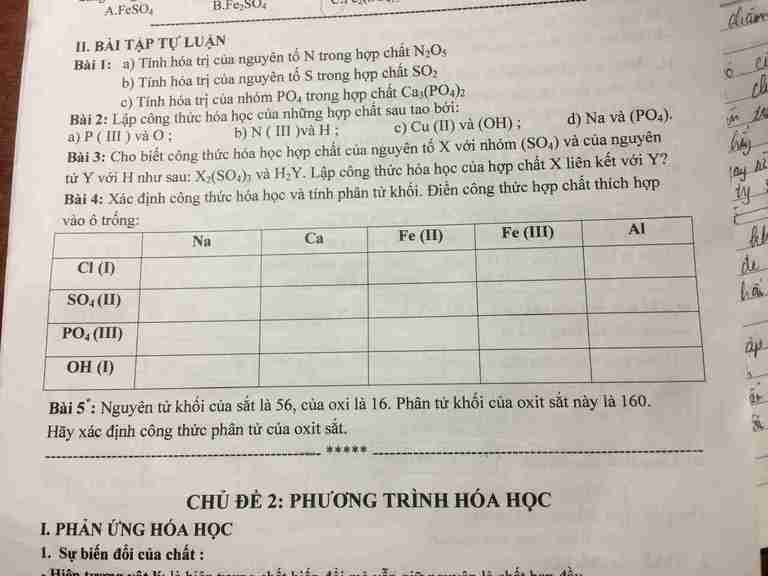
Bài 2: CTHH của câu d là Na3PO4
Bài 4:
| Na | Ca | Fe(II) | Fe(III) | Al | |
| Cl(I) | NaCl 58,5 | CaCl2 111 | FeCl2 127 | FeCl3 162,5 | AlCl3 133,5 |
| SO4 (II) | Na2SO4 142 | CaSO4 136 | FeSO4 152 | Fe2(SO4)3 400 | Al2(SO4)3 342 |
| PO4 (III) | Na3PO4 164 | Ca3(PO4)2 310 | Fe3(PO4)2 358 | FePO4 151 | AlPO4 122 |
| OH (I) | NaOH 40 | Ca(OH)2 74 | Fe(OH)2 90 | Fe(OH)3 107 | Al(OH)3 78 |
GIÚP EM BÀI GIẢI PT VÀ CÂU C,D,E BÀI 2 VỚI Ạ..
\(b,B=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}+\dfrac{\sqrt{x}-8}{x-5\sqrt{x}+6}\left(x\ge0;x\ne4;x\ne9\right)\\ B=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-4+\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-4\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)
\(c,B< A\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\Leftrightarrow\dfrac{\sqrt{x}-4}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}< 0\\ \Leftrightarrow\dfrac{-5}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2>0\left(-5< 0\right)\\ \Leftrightarrow x>4\\ d,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}:\dfrac{\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\sqrt{x}-4}{\sqrt{x}+1}=1-\dfrac{5}{\sqrt{x}+1}\in Z\\ \Leftrightarrow5⋮\sqrt{x}+1\Leftrightarrow\sqrt{x}+1\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\\ \Leftrightarrow\sqrt{x}\in\left\{-6;-2;0;4\right\}\\ \Leftrightarrow x\in\left\{0;16\right\}\left(\sqrt{x}\ge0\right)\)
\(e,P=1-\dfrac{5}{\sqrt{x}+1}\)
Ta có \(\sqrt{x}+1\ge1,\forall x\Leftrightarrow\dfrac{5}{\sqrt{x}+1}\ge5\Leftrightarrow1-\dfrac{5}{\sqrt{x}+1}\le-4\)
\(P_{max}=-4\Leftrightarrow x=0\)
Ai giải giúp mình bài này với giải câu d kĩ một tý ạ
1 oxit kim loại hóa trị 3 là al2o3
dẫn khối lượng 16g h2
pthh 2al2o3 + 6h2-> 4al + 6h2o ( điều kiện phản ứng là nhiệt độ )
d.\(n_{H_2}=0,3mol\) ( đã tính ở câu b )
Gọi kim loại hóa trị III đó là R
\(R_2O_3+3H_2\rightarrow\left(t^o\right)2R+3H_2O\)
0,1 0,3 ( mol )
Ta có:\(n_{R_2O_3}=\dfrac{16}{2M_R+48}\left(mol\right)\)
\(\rightarrow n_{R_2O_3}=\dfrac{16}{2M_R+48}=0,1\)
\(\rightarrow M_R=56\) ( g/mol )
--> R là Sắt (Fe)
giải giúp mình câu d bài 15 với ạ:((
a) Gọi x, y lần lượt là số mol Al, Fe
2Al + 3H2SO4 → Al2(SO4)3 + 3H2
Fe + H2SO4 → FeSO4+ H2
\(\left\{{}\begin{matrix}27x+56y=5,54\\\dfrac{3}{2}x+y=\dfrac{3,584}{22,4}\end{matrix}\right.\)
=> x=0,06 , y =0,07
=> \(m_{Al}=1,62\left(g\right);m_{Fe}=3,92\left(g\right)\)
b) \(n_{H_2SO_4\left(pứ\right)}=n_{H_2}=0,16\left(mol\right)\)
=> \(m_{H_2SO_4\left(pứ\right)}=0,16.98=15,68\left(g\right)\)
c) \(m_{ddH_2SO_4}=\dfrac{15,68}{20\%}=78,4\left(g\right)\)
c) 2NaOH + H2SO4 → Na2SO4 + 2H2O
\(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaOH}=\dfrac{1}{2}.0,25.0,6=0,075\left(mol\right)\)
=> \(m_{H_2SO_4\left(bđ\right)}=15,68+0,075.98=23,03\left(g\right)\)
Giúp mình giải bài 5 phần d với ạ
a, bạn tự sắp xếp nhé
b, Ta có : \(P\left(x\right)+Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x-2x^5+3x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=6x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
Ta có \(P\left(x\right)-Q\left(x\right)\)hay
\(2x^5+3x^4-9x^3-2x^2-\dfrac{1}{4}x+2x^5-3x^4+2x^3-4x^2+\dfrac{1}{4}\)
\(=4x^5-7x^3-6x^2-\dfrac{1}{4}x+\dfrac{1}{4}\)
Giá trị x=0 là nghiệm của P(x) vì ko có hệ số tự do => GT là 0
Cái còn lại 1/4 là hệ số tự do => x=0 ko phải là nghiệm của Q(x)
c, Ta có : \(Q\left(-1\right)=4+3+2+2-\dfrac{1}{4}=11-\dfrac{1}{4}=\dfrac{43}{4}\)
Giải giúp mình câu d bài 4 với ạ!!
Giải giúp mình bài hình câu c , d với ạ
Giúp mik giải bài 2 câu d nhanh với ạ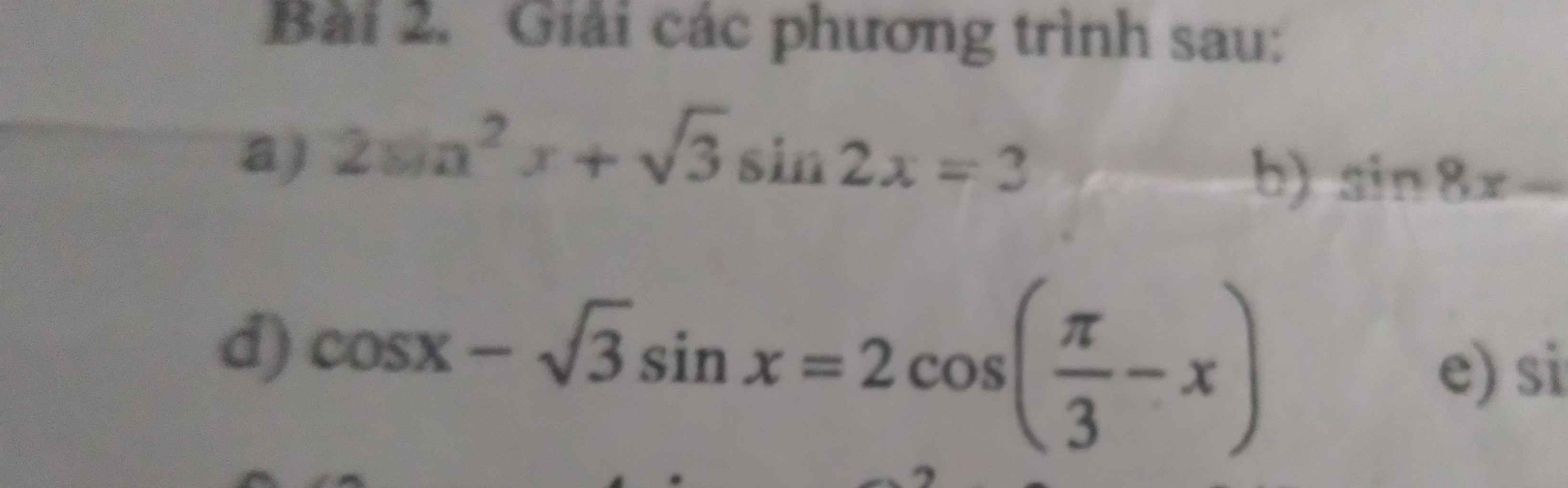
a, \(2sin^2x+\sqrt{3}sin2x=3\)
\(\Leftrightarrow-\left(1-2sin^2x\right)+\sqrt{3}sin2x=2\)
\(\Leftrightarrow\sqrt{3}sin2x-cos2x=2\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sin2x-\dfrac{1}{2}cos2x=1\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{6}\right)=1\)
\(\Leftrightarrow2x-\dfrac{\pi}{6}=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{3}+k\pi\)
d, \(cosx-\sqrt{3}sinx=2cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=cos\left(\dfrac{\pi}{3}-x\right)\)
\(\Leftrightarrow-2sin\dfrac{\pi}{3}.sinx=0\)
\(\Leftrightarrow sinx=0\)
\(\Leftrightarrow x=k\pi\)
d, cosx - \(\sqrt{3}\)sinx = 2cos\(\left(\dfrac{\pi}{3}-x\right)\)
⇔ \(2cos\left(x+\dfrac{\pi}{3}\right)=2cos\left(x-\dfrac{\pi}{3}\right)\)
⇔ \(cos\left(x+\dfrac{\pi}{3}\right)-cos\left(x-\dfrac{\pi}{3}\right)\) = 0
⇔ \(-2sinx.sin\dfrac{\pi}{3}=0\)
⇔ sinx = 0
⇔ x = kπ , k ∈ Z
Sử dụng các công thức sau :
\(cos\left(x+\dfrac{\pi}{3}\right)=cosx.cos\dfrac{\pi}{3}-sinx.sin\dfrac{\pi}{3}=\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx\)
\(cosa-cosb=-2sin\dfrac{a+b}{2}.sin\dfrac{a-b}{2}\)