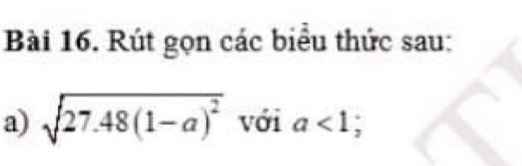
`\sqrt(27 . 48 . (1-a)^2)`

`=\sqrt(1296 . (1-a)^2)`

`= 36 . |1-a|`

`=36(1-a) (a<1 => 1-a >0)`

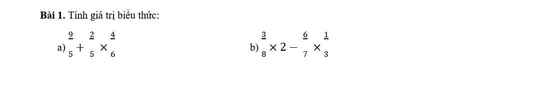
a) 9/5 + 2/5 x 4/6 = 9/5 + 4/15 = 27/15 + 4/15 = 31/15
b) 3/8 x 2 - 6/7 x 1/3 = 3/4 - 2/7 = 21/28 - 8/28 = 13/28

a) 9/5 + 2/5 x 4/6 = 9/5 + 4/15 = 27/15 + 4/15 = 31/15
b) 3/8 x 2 - 6/7 x 1/3 = 3/4 - 2/7 = 21/28 - 8/28 = 13/28

1. They celebrate it in the first month of spring. 

2. People often clean their house. 

3. It means fire.

4. Yes, it is. 

1. They celebrate it in the first month of spring. 

2. People often clean their house. 

3. It means fire.

4. Yes, it is. 

1. It is easy for everyone to get access to the Internet

2.Solar

1 not

2 It is easy for everyone to get access to the internet

3 C

1D

2C

3B

4D

5B

6B

7C

4:

Gọi số xe loại 45 chỗ và 16 chỗ lần lượt là a,b

Có tổng cộng là 9 xe nên a+b=9

Có 289 người tham gia nên 45a+16b=289

Do đó, ta có hệ:

a+b=9 và 45a+16b=289

=>a=5 và b=4

5:

a: Số tiền vốn là:

300000*100=30000000(đồng)

Số tiền thu về là:

30000000+12300000=42300000(đồng)

b; Gọi số tiền cửa hàng bán 1 chiếc áo vào thời điểm khuyến mãi là x

=>Số tiền vốn là x:0,7=10/7x

Theo đề, ta có:

10/7x*80+x*20=42300000

=>x=315000

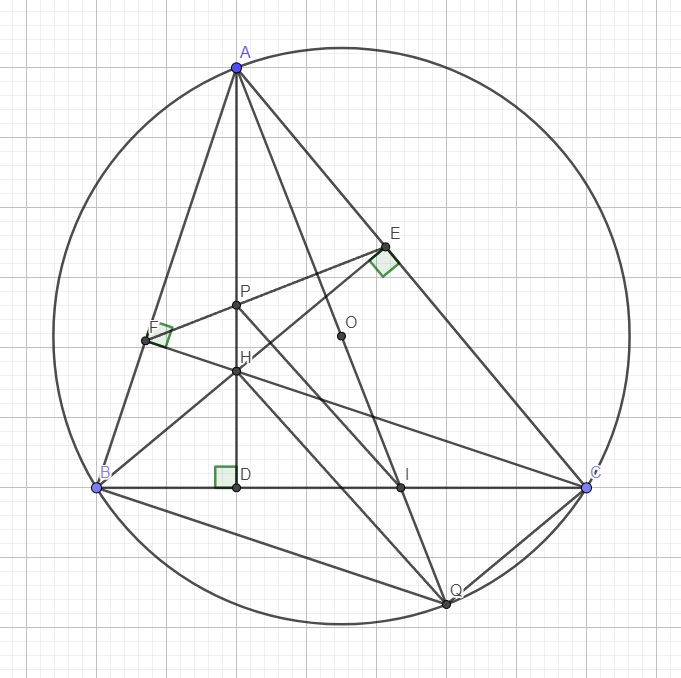
a. Em tự giải

b.

Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)

Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn

\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)

Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)

(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)

c.

\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)

Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)

\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)

Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)

\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)

(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)

\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)

AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)

Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\)  \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)

\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)

(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)

\(\Rightarrow PI||HQ\) (định lý Talet đảo)