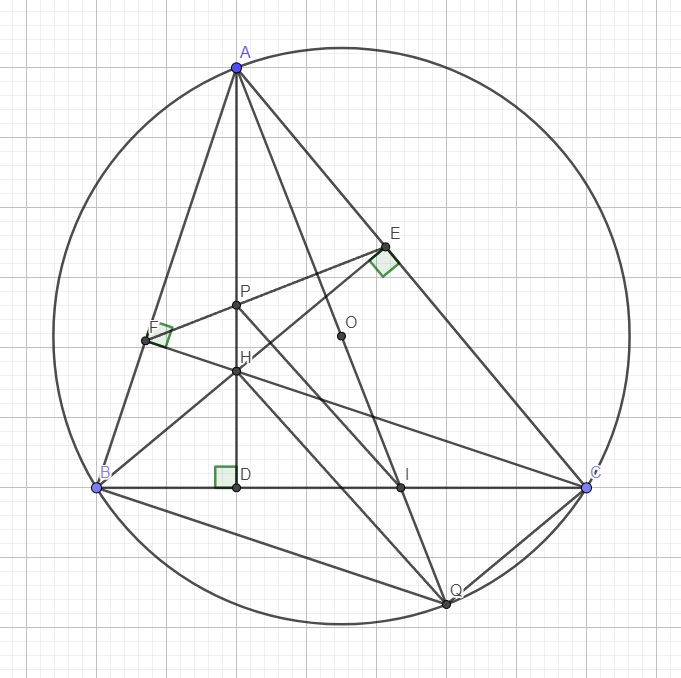
a. Em tự giải
b.
Ta có: \(\widehat{ABC}=\widehat{AQC}\) (cùng chắn AC) (1)
Do AQ là đường kính \(\Rightarrow\widehat{ACQ}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACQ}=90^0\) \(\Rightarrow\widehat{ACQ}+\widehat{CAQ}=90^0\) (2)
Tam giác ABD vuông tại D \(\Rightarrow\widehat{BAD}+\widehat{ABC}=90^0\) (3)
(1);(2);(3) \(\Rightarrow\widehat{CAQ}=\widehat{BAD}\)
c.
\(\left\{{}\begin{matrix}\widehat{PAE}=\widehat{PAI}+\widehat{CAQ}\\\widehat{IAB}=\widehat{PAI}+\widehat{BAD}\\\widehat{CAQ}=\widehat{BAD}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{PAE}=\widehat{IAB}\) (3)
Tứ giác BCEF nội tiếp (E và F cùng nhìn BC dưới 1 góc vuông)
\(\Rightarrow\widehat{ABI}+\widehat{CEF}=180^0\)
Mà \(\widehat{CEF}+\widehat{AEP}=180^0\)
\(\Rightarrow\widehat{AEP}=\widehat{ABI}\) (4)
(3);(4) \(\Rightarrow\Delta AEP\sim\Delta ABI\left(g.g\right)\)
\(\Rightarrow\dfrac{AP}{AI}=\dfrac{AE}{AB}\) (5)
AQ là đường kính \(\Rightarrow\widehat{ABQ}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ABQ}=90^0\)
Xét 2 tam giác ABQ và AEH có: \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{AEH}=90^0\\\widehat{BAQ}=\widehat{EAH}\left(\text{theo (3)}\right)\end{matrix}\right.\) \(\Rightarrow\Delta ABQ\sim\Delta AEH\left(g.g\right)\)
\(\Rightarrow\dfrac{AE}{AB}=\dfrac{AH}{AQ}\) (6)
(5);(6) \(\Rightarrow\dfrac{AH}{AQ}=\dfrac{AP}{AI}\) \(\Rightarrow\dfrac{AP}{AH}=\dfrac{AI}{AQ}\)
\(\Rightarrow PI||HQ\) (định lý Talet đảo)