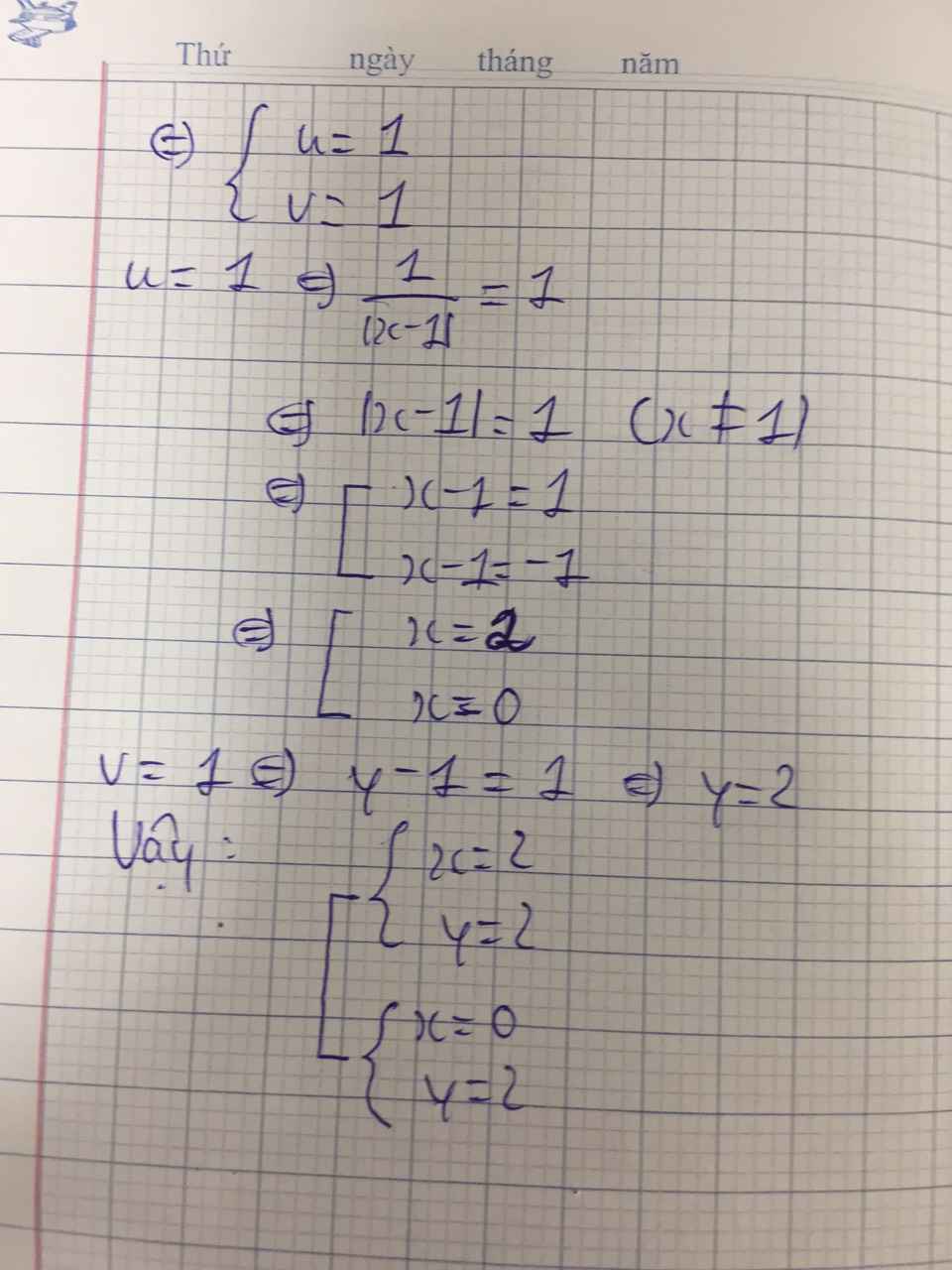Giải phương trình sau: \(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\))

Những câu hỏi liên quan
Giải phương trình: \(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\)
Giải các phương trình sau:
a) \(\left(4-x\right)^5+\left(x-2\right)^5=32\)
b) \(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\)
Mk chỉ làm đc câu a) thôi còn câu b mk cũng đang hỏi.
Đặt \(4-x=a\); \(x-2=b\) \(\Rightarrow\) \(a+b=2\)
\(\Leftrightarrow\)\(\left(a^3+b^3\right)\left(a^2+b^2\right)-a^2b^2\left(a+b\right)=32\)
\(\Leftrightarrow\)\(\left[\left(a+b\right)^3-3ab\left(a+b\right)\right]\left[\left(a+b\right)^2-2ab\right]-a^2b^2\left(a+b\right)=32\)
thay \(a+b=2\) ta có:
\(\left(8-6ab\right)\left(4-2ab\right)-2\left(ab\right)^2=32\)
\(\Leftrightarrow\) \(32-40ab+10\left(ab\right)^2=32\)
\(\Leftrightarrow\)\(10ab\left(-4+ab\right)+32-32=0\)
\(\Leftrightarrow\)\(ab\left(ab-4\right)=0\)
\(\Leftrightarrow\)\(\left[{}\begin{matrix}ab=0\\ab-4=0\end{matrix}\right.\)
Với \(ab=0\) thì \(\left(4-x\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(\left[{}\begin{matrix}4-x=0\\x-2=0\end{matrix}\right.\) \(\Rightarrow\) \(\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
Với \(ab-4=0\) thì \(\left(4-x\right)\left(x-2\right)-4=0\)
\(\Leftrightarrow\)\(6x-8-x^2-4=0\)
\(\Leftrightarrow\)\(6x-12-x^2=0\)
\(\Leftrightarrow\)\(-\left(x^2-6x+12\right)=0\)
\(\Leftrightarrow\)\(-\left(x^2-6x+9+3\right)=0\)
\(\Leftrightarrow\)\(-\left(x-3\right)^2-3=0\) ( vô lí )
Vậy pt có tập nghiệm \(S=\left\{2;4\right\}\)
Giải phương trình: \(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\)
giải phương trình:
\(\left(x-1\right)^5+\left(x+3\right)^5=242\left(x+1\right)\)
Giải phương trình \(\dfrac{3\left(x-\sqrt{3}\right)\left(x-\sqrt{5}\right)}{\left(1-\sqrt{3}\right)\left(1-\sqrt{5}\right)}+\dfrac{4\left(x-1\right)\left(x-\sqrt{5}\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}-\sqrt{5}\right)}+\dfrac{5\left(x-1\right)\left(x-\sqrt{3}\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}=3x-2\)
Bài Toán :
Giải phương trình sau :
\(\frac{3\left(x-\sqrt{3}\right)\left(x-\sqrt{5}\right)}{\left(1-\sqrt{3}\right)\left(1-\sqrt{5}\right)}+\frac{4.\left(x-1\right)\left(x-\sqrt{5}\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}-\sqrt{5}\right)}+\frac{5\left(x-1\right)\left(x-\sqrt{3}\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}-\sqrt{3}\right)}=3x-2\)
Giải hệ phương trình sau: \(\left\{{}\begin{matrix}\dfrac{2}{\left|x-1\right|}-5\left(y-1\right)=-3\\\dfrac{1}{\left|x-1\right|}-2\left(1-y\right)=3\end{matrix}\right.\)
Giải các bất phương trình sau :
\(a.4\left(x-3\right)^2-\left(2x-1\right)^2\ge12\)
\(b.\left(x-4\right)\left(x+4\right)\ge\left(x+3\right)^2+5\)
c. \(\left(3x-1\right)^2-9\left(x+2\right)\left(x-2\right)< 5x\)
\(a,4\left(x-3\right)^2-\left(2x-1\right)^2\ge12\)
\(\Leftrightarrow4x^2-24x+36-4x^2-4x+1\ge12\)
\(\Leftrightarrow-28x+37\ge12\)
\(\Leftrightarrow-28x\ge12-37\)
\(\Leftrightarrow-28x\ge-25\)
\(\Leftrightarrow x\le\dfrac{25}{28}\)
Vậy \(S=\left\{x\left|x\le\dfrac{25}{28}\right|\right\}\)
b, \(\left(x-4\right)\left(x+4\right)\ge\left(x+3\right)^2+5\)
\(\Leftrightarrow x^2-16\ge x^2+6x+9+5\)
\(\Leftrightarrow x^2-x^2-6x\ge9+5+16\)
\(\Leftrightarrow-6x\ge30\)
\(\Leftrightarrow x\le-5\)
Vậy \(S=\left\{x\left|x\le-5\right|\right\}\)
\(c,\left(3x-1\right)^2-9\left(x+2\right)\left(x-2\right)< 5x\)
\(\Leftrightarrow9x^2-6x-1-9x^2+36< 5x\)
\(\Leftrightarrow9x^2-9x^2-6x-5x+36+1< 0\)
\(\Leftrightarrow-11x+37< 0\)
\(\Leftrightarrow-11x< -37\)
\(\Leftrightarrow x>\dfrac{37}{11}\)
vậy \(S=\left\{x\left|x>\dfrac{37}{11}\right|\right\}\)
Đúng 1
Bình luận (0)
GIẢI PHƯƠNG TRÌNH SAU: \(5\left(x-1\right)\left(x-5\right)\left(x-3\right)\left(x-15\right)=7x^2\)