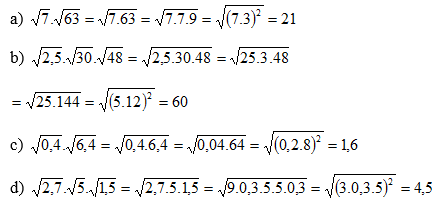A=\(\sqrt{0,1}+\sqrt{0,9}+\sqrt{6,4}+\sqrt{0.4}+\sqrt{44,1}\)

Những câu hỏi liên quan
Thực hiện phép tính:
a)\(\sqrt{49}+\sqrt{25}-4\cdot0,25\)
b)\(\sqrt{\frac{1}{9}}\cdot\sqrt{0.81}\cdot\sqrt{0,9}\)
c)\(\sqrt{6,4\cdot2400\cdot0,6}\)
d)\(\sqrt{26^2-24^2}\)
a) \(\sqrt{49}+\sqrt{25}-4\cdot0,25\)
\(=7+5-1=11\)
b) \(\sqrt{\frac{1}{9}}\cdot\sqrt{0,81}\cdot\sqrt{0,9}\)
\(=\frac{1}{3}\cdot\frac{9}{10}\cdot\frac{3\sqrt{10}}{10}\)
\(=\frac{9\sqrt{10}}{100}\)
c) \(\sqrt{6,4\cdot2400\cdot0,6}\)
\(=\sqrt{64\cdot36\cdot4}\)
\(=8\cdot6\cdot2=96\)
d) \(\sqrt{26^2-24^2}=\sqrt{\left(26-24\right)\left(26+24\right)}\)
\(=\sqrt{2\cdot50}=\sqrt{100}=10\)
Tính:
\(\begin{array}{l}a)2.\sqrt 6 .( - \sqrt 6 );\\b)\sqrt {1,44} - 2.{(\sqrt {0,6} )^2};\\c)0,1.{(\sqrt 7 )^2} + \sqrt {1,69} ;\\d)( - 0,1).{(\sqrt {120} )^2} - \frac{1}{4}.{(\sqrt {20} )^2}\end{array}\)
\(\begin{array}{l}a)2.\sqrt 6 .( - \sqrt 6 )\\ = - 2.\sqrt 6 .\sqrt 6 \\ = - 2.{(\sqrt 6 )^2}\\ = - 2.6\\ = - 12\\b)\sqrt {1,44} - 2.{(\sqrt {0,6} )^2}\\ = 1,2 - 2.0,6\\ = 1,2 - 1,2\\ = 0\\c)0,1.{(\sqrt 7 )^2} + \sqrt {1,69} \\ = 0,1.7 + 1,3 \\= 0,7 + 1,3 \\= 2\\d)( - 0,1).{(\sqrt {120} )^2} - \frac{1}{4}.{(\sqrt {20} )^2} \\= ( - 0,1).120 - \frac{1}{4}.20\\ = - 12 - 5\\ = - (12 + 5)\\ = - 17\end{array}\)
Đúng 0
Bình luận (0)
a: \(=-2\sqrt{6}\cdot\sqrt{6}=-2\cdot\sqrt{6\cdot6}=-2\cdot6=-12\)
b: \(=1.2-2\cdot0.6=1.2-1.2=0\)
c: \(=0.1\cdot7+1.3=0.7+1.3=2\)
d: \(=-0.1\cdot120-\dfrac{1}{4}\cdot20=-12-5=-17\)
Đúng 0
Bình luận (0)
(\(\sqrt{8}-3\sqrt{2}+\sqrt{10}\)) . (\(\sqrt{2}-3\sqrt{0.4}\))
giải cụ thể giúp mk vớiiiii ạ
\(=4-\dfrac{12}{5}\sqrt{5}-6+\dfrac{18}{5}\sqrt{5}+2\sqrt{5}-6\)
\(=-8+\dfrac{16}{5}\sqrt{5}\)
Đúng 0
Bình luận (0)
i,\(\sqrt{12,1.360}\)
k,\(\sqrt{0,4}.\sqrt{6,4}\)
l,-0,4\(\sqrt{\left(-0,4\right)^2}\)
m,\(\sqrt{2^4.\left(-7\right)^2}\)
\(i,\sqrt{12,1.360}=\sqrt{12,1}.6\sqrt{10}=6.\sqrt{12,1.10}=6.\sqrt{121}=6.\sqrt{11^2}=6.11=66\)
\(k,\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{\dfrac{64}{25}}=\dfrac{\sqrt{8^2}}{\sqrt{5^2}}=\dfrac{8}{5}\)
\(l,-0,4.\sqrt{\left(-0,4\right)^2}=-0,4.0,4=-0,16\)
\(m,\sqrt{2^4.\left(-7\right)^2}=\sqrt{4^2}.\sqrt{\left(-7\right)^2}=4.7=28\)
Đúng 4
Bình luận (2)
i, \(\sqrt{12,1\cdot360}=\sqrt{4356}=\sqrt{66^2}=66\)
k, \(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4\cdot6,4}=\sqrt{\dfrac{64}{25}}=\sqrt{\dfrac{2^6}{5^2}}=\dfrac{2^3}{5}=\dfrac{8}{5}\)
l, \(-0,4\sqrt{\left(-0,4\right)^2}=-0,4\cdot\left|-0,4\right|=-0,4\cdot0,4=-\dfrac{4}{25}\)
m, \(\sqrt{2^4\cdot\left(-7\right)^2}=2^2\cdot\left|-7\right|=4\cdot7=28\)
Đúng 1
Bình luận (0)
i) \(\sqrt{12,1.360}=\sqrt{12,1}.\sqrt{360}=\sqrt{12,1}.\sqrt{36}.\sqrt{10}=\left(\sqrt{12,1}.\sqrt{10}\right)\sqrt{36}=\sqrt{121}.\sqrt{36}=11.6=66\)
k) \(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{2,56}=1,6\)
l) \(-0,4\sqrt{\left(-0,4\right)^2}=-0,4\left|-0,4\right|=-0,4.0,4=0,16\)
m) \(\sqrt{2^4.\left(-7\right)^2}=\sqrt{2^2.2^2.\left(-7\right)^2}=\left|2.2.7\right|=28\)
Đúng 1
Bình luận (1)
Tính
\(\sqrt{0,4}\cdot\sqrt{6,4}-\sqrt{2,7}\cdot\sqrt{5}\cdot\sqrt{1,5}\)
Tính giá trị của biểu thức:
\(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} ;b)\sqrt {0,36} - \sqrt {0,81} ;\\c)8.\sqrt 9 - \sqrt {64} ;d)0,1.\sqrt {400} + 0,2.\sqrt {1600} \end{array}\)
\(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} = 0,7 + 0,8 = 1,5;\\b)\sqrt {0,36} - \sqrt {0,81} = 0,6 - 0,9 = - 0,3;\\c)8.\sqrt 9 - \sqrt {64} = 8.3 - 8 = 24 - 8 = 16;\\d)0,1.\sqrt {400} + 0,2.\sqrt {1600} = 0,1.20 + 0,2.40 = 2 + 8 = 10\end{array}\)
Đúng 1
Bình luận (0)
Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a. \(\sqrt{7}.\sqrt{63};\)
b. \(\sqrt{2,5}.\sqrt{30}.\sqrt{48};\)
c. \(\sqrt{0,4}.\sqrt{6,4};\)
d. \(\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}.\)
Ta thấy các số trong căn bậc hai đều lớn hơn 0, áp dụng \(\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}\)
a) \(\sqrt{7}\cdot\sqrt{63}=\sqrt{7\cdot63}=21\)
b) \(\sqrt{2,5}\cdot\sqrt{30}\cdot\sqrt{48}=\sqrt{2,5\cdot30\cdot48}=60\)
c) \(\sqrt{0,4}\cdot\sqrt{6,4}=\sqrt{0,4\cdot6,4}=1,6\)
d) \(\sqrt{2,7}\cdot\sqrt{5}\cdot\sqrt{1,5}=\sqrt{2,7\cdot5\cdot1,5}=4,5\)
Đúng 0
Bình luận (0)
a. \(\sqrt{7}.\sqrt{63}=\sqrt{7.63}=\sqrt{441}=21\)
b.\(\sqrt{2,5}.\sqrt{30}.\sqrt{48}=\sqrt{2,5.30.48}=\sqrt{3600}=60\)
c.\(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{2,56}=1,6\)
d.\(\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}=\sqrt{2,7.5.1,5}=\sqrt{20,25}=4,5\)
Đúng 0
Bình luận (0)
\(\sqrt{7}.\sqrt{63}=\sqrt{7.63}=\sqrt{441}=21\)
\(\sqrt{2,5}.\sqrt{30}.\sqrt{48}=\sqrt{2,5.30.48}=\sqrt{3600}=60\)
\(\sqrt{0,4}.\sqrt{6,4}=\sqrt{0,4.6,4}=\sqrt{2,56}=1,6\)
\(\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}=\sqrt{2,7.5.1,5}=\sqrt{20,25}=4,5\)
Đúng 0
Bình luận (0)
Bài 18 (trang 14 SGK Toán 9 Tập 1)
Áp dụng quy tắc nhân các căn bậc hai, hãy tính:
a) $\sqrt{7}.\sqrt{63}$ ; b) $\sqrt{2,5}.\sqrt{30}.\sqrt{48}$ ;
c) $\sqrt{0,4}\sqrt{6,4}$ ; d) $\sqrt{2,7}.\sqrt{5}.\sqrt{1,5}$.
a)\(\sqrt{7.63}\)=21
b)\(\sqrt{2,5.30.48}\)=60
c)\(\sqrt{0,4.6,4}\)=1,6
d)\(\sqrt{2,7.5.1,5}\)=4,5
a) .
b)
.
c)
.
d)
.
Xem thêm câu trả lời
\(\sqrt{0.4}+\sqrt{2.5}\)
\(\sqrt{0,4}+\sqrt{2,5}\)
\(=\sqrt{10}\left(\sqrt{0,04}+\sqrt{0,25}\right)\)
\(=\sqrt{10}\left(0,2+0,5\right)\)
\(=\sqrt{10}.\frac{7}{10}=\frac{7}{\sqrt{10}}\)
Đúng 0
Bình luận (1)