Cho tứ giác ABDC có A,B,C,D thuộc đường tròn tâm O;có AB<CD;AC<BD,AB cắt CD tại M,AC cắt BD tại N,tia phân giác góc AMC cắt tia phân giác góc ANB tại I. cmr: I thuộc đường tròn đường kính MN

Những câu hỏi liên quan
Cho đường tròn (O) có đường kính Ab và C thuộc đường tròn đó ( C khác A,B ) . Lấy điểm D thuộc dây BC ( D khác B,C ) . Tia AD cắt cung nhỏ BC tại E, Tia AC cắt tia BE tại M
a. Chứng minh tứ giác CDEM nội tiếp được đường tròn .Xác định tâm I Của đường tròn ngoại tiếp tứ giác CDEM
b.Chứng minh : AD.ED=BD.CD
c. Chứng Minh IC là tiếp tuyến của đường tròn tâm (O)
Cho đường tròn tâm O đường kính AD. Vẽ dây BC vuông góc với AD. Vẽ đường tròn tâm D bán kính DB. Lấy điểm F trên cung BC. Tiếp tuyến tại F của đường tròn tâm D cắt AB, AC theo thứ tứ tại M và N.
a) Chứng minh rằng tứ giác ABDC nội tiếp
b) Chứng minh rằng BM + CN = MN
a: Vì A,B,D,C cùng nằm trên (O)
nên ABDC nội tiếp
b: Xét (D) có
MB,MF là tiếp tuyến
=>MB=MF
Xét (D) có
NF,NC là tiếp tuyến
=>NF=NC
=>MB+CN=MF+NF=MN
Đúng 0
Bình luận (0)
Cho đường tròn tâm O , đường thẳng d cắt đường tròn tâm O tại A và B . Từ điểm M thuộc d kẻ tiếp tuyến MC và MD của đường tròn a) chứng minh tứ giác MCOD nội tiếp b) chứng minh tam giác MCA đồng dạng tam giác MBC c) chứng minh AC.BD=AD.BC
a: Xét tứ giác MCOD có \(\widehat{MCO}+\widehat{MDO}=180^0\)
nên MCOD là tứ giác nội tiếp
b: Xét ΔMCA và ΔMBC có
\(\widehat{MCA}=\widehat{MBC}\)
\(\widehat{AMC}\) chung
Do đó; ΔMCA\(\sim\)ΔMBC
Đúng 0
Bình luận (0)
Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn đó(C khác A,B).Lấy điểm D thuộc dây BC (D khác B,C).Tia AD cắt cung nhỏ BC tại điểm E,tia AC cắt tia BE tại điểm F
a)CM:tứ giác FCDE là tứ giác nội tiếp đường tròn
b)CM:DA.DE =DB.DC
c)Gọi I là tâm đường tròn ngoại tiếp tứ giác FCDE,CM:IC là tiếp tuyến của đường tròn (O)
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC
Đúng 0
Bình luận (0)
Cho tam giác đều ABC. Trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy điểm D sao cho DB = DC và DCB ^ = 1 2 ACB ^
a) Chứng minh tứ giác ABDC là tứ giác nội tiếp.
b) Xác định tâm của đường tròn đi qua bốn điểm A, B, D, C.
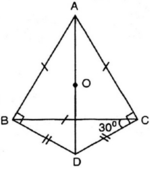

⇒ AD là đường kính của đường tròn ngoại tiếp tam giác ABD Mà ABDC là tứ giác nội tiếp
⇒ AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC.
⇒ tâm O là trung điểm AD.
Vậy tâm đường tròn đi qua bốn điểm A, B, D, C là trung điểm AD.
Kiến thức áp dụng
+ Một tứ giác có tổng số đo hai góc đối nhau bằng 180º thì tứ giác đó nội tiếp được đường tròn.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông.
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, có hai đường cao BB' và CC' cắt nhau tại H a)Chứng minh tứ giác BCB'C' nội tiếp? b)Gọi H' là đối xứng của H qua BC. Chứng minh H thuộc đường tròn tâm O? c)Tia AO cắt đường tròn tâm O tại D và cắt B'C' tại I. Chứng minh AD vông góc với C'B'
a) Xét tứ giác BCB'C' có
\(\widehat{BC'C}=\widehat{BB'C}\left(=90^0\right)\)
\(\widehat{BC'C}\) và \(\widehat{BB'C}\) là hai góc cùng nhìn cạnh BC
Do đó: BCB'C' là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O có đường kính AB và C là một điểm thuộc đường tròn tâm O (C khác A,B). Lấy điểm D thuộc dây cung BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE tại điểm F. Chứng minh:
a) Tứ giác FCDE nội tiếp
b) Chứng minh DA.DE = DB.DC
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC
Đúng 1
Bình luận (0)
a: góc ACB=góc AEB=1/2*180=90 độ
=>CB vuông góc FA,AE vuông góc FB
góc FCD+góc FED=180 độ
=>FCDE nội tiếp
b: Xét ΔDCA vuông tại C và ΔDEB vuông tại E có
góc CDA=góc EDB
=>ΔDCA đồng dạng với ΔDEB
=>DC/DE=DA/DB
=>DA*DE=DB*DC
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn (AB AC) nội tiếp đường tròn (O ; R). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M. Gọi I là trung điểm của BC.a, Chứng minh tứ giác MAOI nội tiếp trong một đường tròn. Xác định tâm và đường kính của đường tròn này.b, Chứng minh: MA2 MB.MCc, Vẽ đường kính AK của đường tròn (O). Gọi H là điểm đối xứng của K qua I. Chứng minh H là trực tâm của tam giác ABC.d, Tia AH cắt (O) tại D. Cho BI ( R √6)/3 và góc ABC – ACB 30o . Tính điện tích của tứ giác A...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn (AB < AC) nội tiếp đường tròn (O ; R). Tiếp tuyến tại A của đường tròn (O) cắt đường thẳng BC tại M. Gọi I là trung điểm của BC.
a, Chứng minh tứ giác MAOI nội tiếp trong một đường tròn. Xác định tâm và đường kính của đường tròn này.
b, Chứng minh: MA2 = MB.MC
c, Vẽ đường kính AK của đường tròn (O). Gọi H là điểm đối xứng của K qua I. Chứng minh H là trực tâm của tam giác ABC.
d, Tia AH cắt (O) tại D. Cho BI =( R √6)/3 và góc ABC – ACB = 30o . Tính điện tích của tứ giác ABDC theo R.
Cho △ABC nhọn (AB<AC) nội tiếp (O), 2 đường cao BD và CE cắt nhau tại H
a/ Chứng minh : B,C,D,E cùng nằm trên một đường tròn .Xác định tâm M của đường tròn này.
b/ Chứng minh : OM // AH
c/ Chứng minh : AB.AE = AC.AD
d/ Gọi K là điểm đối xứng của H qua M .
1 cho đường tròn tâm O có đường kính AB và điểm C thuộc đường tròn đó (C khác A, B). Lấy điểm D thuộc dây BC tại điểm E, tia AC cắt tia BE tại điểm F
a, cmr FCDE là tứ giác nội tiếp đường tròn
b, cmr DA . DE = DB . DC
c, gọi I là tâm của đường tròn ngoại tiếp tam giác FCDE, cmr IC là tiếp tuyến














