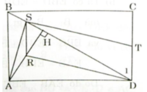
a) Hai tam giác vuông AHD và BDC có ∠ADH = ∠CBD (SLT)

⇒ ΔAHD ∼ ΔDCB (g.g)

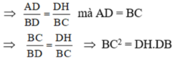
b) Ta có S, R là trung điểm của HB và AH nên SR là đường trung bình của ΔABH ⇒ SR // AB

⇒ ∠HSR = ∠HBA (đồng vị)

Mà ∠HBA = ∠D1

⇒ HSR = ∠D1

Do đó ΔSHR ∼ ΔDCB (g.g)

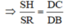
c) Ta có SR // AB và SR = AB/2 (cmt), TD = CD/2

mà AB = CD và AB // CD (gt)

⇒ SR // DT và SR = DT

Do đó Tứ giác DRST là hình bình hành

d) Ta có SR // AB mà AB ⊥ AD (gt) ⇒ SR ⊥ AD, lại có AH ⊥ SD (gt)

⇒ R là trực tâm của ΔSAD ⇒ DR là đường cao thứ ba nên DR ⊥ SA

Mà DR // ST (DRST là hình bình hành) ⇒ ST ⊥ SA

Vậy ∠AST = 90o

a: Xét ΔABD vuông tại A có AH là đường cao

nên \(AD^2=DH\cdot DB=BC^2\)

c: Xét ΔHAB có

R là trung điểm của HA

S là trung điểm của HB

Do đó: RS là đường trung bình

=>RS//AB và RS=AB/2

=>RS//DT và RS=DT

=>RSTD là hình bình hành

a: Xét ΔHAD có HM/HA=HN/HD

nên MN//AD

 b: Xét ΔHAD có MN//AD

nên MN/AD=HM/HA=1/2

=>MN=1/2AD=1/2BC

=>MN=BI

mà MN//BI

nên BMNI là hình bình hành

a: Xét ΔHAB có 

N là trung điểm của HB

M là trung điểm của HA

Do đó: NM là đường trung bình của ΔAHB

Suy ra: \(NM=\dfrac{AB}{2}=2\left(cm\right)\)

a: Xét tứ giác MFCE có 

\(\widehat{MFC}=\widehat{MEC}=\widehat{FCE}=90^0\)

Do đó: MFCE là hình bình hành

Suy ra: MC=EF

khó quá !!!!!!!!!!!!!!1

Giải chi tiết:

a) Xét tam giác AHD có:

M là trung điểm của AH (gt) 

N là trung điểm của DH (gt) 

Do đó MN là đường trung bình của tam giác AHD

Suy ra MN//AD (tính chất) (đpcm)

b) Ta có MN//AD, mà AD//BC (2 cạnh đối hình chữ nhật)  nên MN//BC hay MN//BI     Vì MN = 1212AD (tính chất đường trung bình của tam giác)    và BI = IC = 1212BC (do gt),  mà AD = BC (2 cạnh đối hình chữ nhật)  MN = BI BC hay MN//BI   Xét tứ giác BMNI có MN//BI, MN = BI (c/m trên)    Suy ra tứ giác BMNI là hình bình hành (đpcm)  

c) Ta có MN//AD và AD⊥⊥AB nên MN⊥⊥AB

Tam giác ABN có 2 đường cao là AH và NM cắt nhau tại M nên M là trực tâm của tam giác ABN. Suy ra BM⊥⊥AN.

Mà BM//IN nên AN⊥⊥NI hay ΔANIΔANI  vuông tại N (đpcm)   

# M̤̮èO̤̮×͜×L̤̮ườI̤̮◇

a) Xét tam giác AHD, có: 
* M,N lần lượt là trung điểm của AH, DH (gt)
=> MN là đường trung bình của tam giác AHD
=> MN // AD (t/c) (đpcm)

b) Ta có: BC // AD (ABCD là hình chữ nhật)
=> MN // BI (I thuộc BC) (1)

Ta lại có: I là trung điểm BC (gt)
=> BI = AD : 2 (BC = AD)
Mà MN = AD :2 (MN là đường trung bình tam giác AHD)
=> BI = MN (2)

Từ (1), (2) => MBIN là hình bình hành (đpcm)

c) Xét tam giác AHN vuông tại N có:
* NM là trung tuyến (M là trung điểm AH)
=> NM = MA = MH (hệ quả)
=> tam giác AMN là tam giác cân tại M
Mà MB là đường nối từ đỉnh của tam giác cân AMN
=> MB là đường cao của tam giác AMN
=> góc AMB = 90 độ
=> AD vuông góc với MB
Mà MB // ID (MDIB là hình bình hành)
=> ID vuông góc với AD
=> góc ANI = 90 độ

P/S: Không chắc câu c) cho lắm.