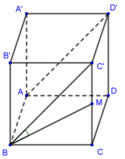
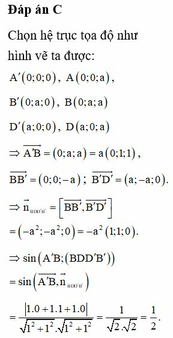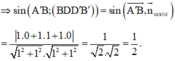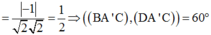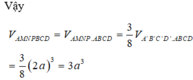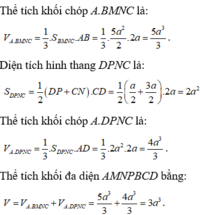Cho hình lập phương abcd.a'b'c'd' có cạnh bằng 2a tính góc giữa CC' và mặt phẳng AB'C'

Những câu hỏi liên quan
Cho hình lập phương ABCD.ABCD có cạnh bằng a, gọi
α
là góc giữa đường thẳng AB và mặt phẳng (BBDD). Tính
sin
α
.
A.
3
4
.
B.
3
2
.
C.
3
5
.
D. ...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a, gọi α là góc giữa đường thẳng AB' và mặt phẳng (BB'D'D). Tính sin α .
A. 3 4 .
B. 3 2 .
C. 3 5 .
D. 1 2 .
Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
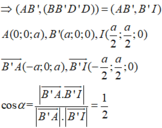
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, gọi
α
là góc giữa đường thẳng
A
B
và mặt phẳng
B
B
D
D
. Tính
sin
α
.
A. ...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α .
A. 3 5 .
B. 3 2 .
C. 1 2 .
D. 3 4 .
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng a, gọi
α
là góc giữa đường thẳng
A
B
và mặt phẳng
B
B
D
D
. Tính
sin
α
A.
3...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α
A. 3 5
B. 3 2
C. 1 2
D. 3 4
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Sin của góc tạo bởi giữa hai mặt phẳng (BDA') và (ABCD) bằng
A. 3 3
B. 6 3
C. 3 4
D. 6 4
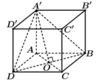
Gọi ![]()
Ta chứng minh được ![]()
Từ (1) và (2) suy ra ![]()
Vậy ![]()
Chọn B
Đúng 0
Bình luận (0)
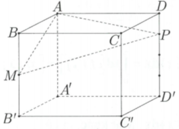
Cho hình lập phương ABCD.ABCD cạnh 2a, gọi M là trung điểm của BB và P thuộc cạnh sao cho
D
P
1
4
D
D
. Mặt phẳng (AMP) cắt CC tại N. Thể tích khối đa diện AMNPBCD bằng
Đọc tiếp
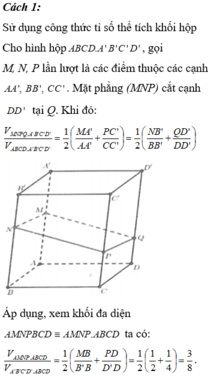
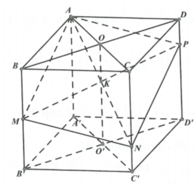
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng

![]()
![]()
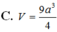

Cho hình lập phương ABCD.ABCD có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là A.
90
0
B.
60
0
C.
30
0
D.
45
0
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Số đo của góc giữa hai mặt phẳng (BA’C) và (DA’C) là
A. 90 0
B. 60 0
C. 30 0
D. 45 0
Cho hình lập phương ABCD.ABCD cạnh 2a, gọi M là trung điểm của BB và P thuộc cạnh DD sao cho
D
P
1
4
D
D
. Mặt phẳng (AMP) cắt CC tại N. Thể tích khối đa diện AMNPBCD bằng A.
V
2
a
3
B.
V
3
a
3
C.
V...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh 2a, gọi M là trung điểm của BB' và P thuộc cạnh DD' sao cho D P = 1 4 D D ' . Mặt phẳng (AMP) cắt CC' tại N. Thể tích khối đa diện AMNPBCD bằng
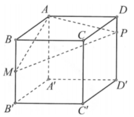
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 a 3 4
D. V = 11 a 3 3
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh 2a, gọi M là trung điểm của
B
B
và P thuộc cạnh
D
D
sao cho
D
P
1
4
D
D...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh 2a, gọi M là trung điểm của B B ' và P thuộc cạnh D D ' sao cho D P = 1 4 D D ' . Mặt phẳng A M P cắt C C ' tại N. Thể tích khối đa diện A M N P B C D bằng
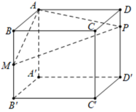
A. V = 2 a 3
B. V = 3 a 3
C. V = 9 a 3 4
D. V = 11 a 3 3
Đáp án B
Áp dụng công thức tính nhanh, ta có V A M P B C D V A B C D . A ' B ' C ' D ' = 1 2 B M B B ' + D P D D ' = 3 8 ⇒ V A M P B C D = 3 a 3 .
Đúng 0
Bình luận (0)
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có các cạnh bằng 1. M là trung điểm CC. Tính góc giữa hai đường thẳng AD và BM. A.
45
°
B.
18
°
26
C.
26
°
33
D.
18
°
43
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có các cạnh bằng 1. M là trung điểm CC'. Tính góc giữa hai đường thẳng AD' và BM.
A. 45 °
B. 18 ° 26 '
C. 26 ° 33 '
D. 18 ° 43 '