Cho ΔABC∼ΔA′B′C′ΔABC∼ΔA′B′C′ theo tỉ số đồng dạng là 2; ΔABC∼ΔA′′B′′C′′theo tỉ số đồng dạng là 5. Vậy thì ΔA′B′C′∼ΔA′′B′′C′′ΔA′B′C′∼ΔA″B″C″ theo tỉ số đồng dạng là bao nhiêu?
A 2/5
B 7
C 3
D 2.
ΔA'B'C' 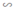 ΔA''B''C'' theo tỉ số đồng dạng k1, ΔA''B''C''
ΔA''B''C'' theo tỉ số đồng dạng k1, ΔA''B''C''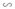 ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
ΔABC theo tỉ số đồng dạng k2. Hỏi tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số nào?
ΔA'B'C' 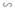 ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒
ΔA''B''C'' theo tỉ số đồng dạng k1 ⇒ 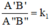
ΔA''B''C'' 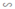 ΔABC theo tỉ số đồng dạng k2 ⇒
ΔABC theo tỉ số đồng dạng k2 ⇒ 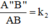
Mà ΔA'B'C' 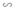 ΔA''B''C''; ΔA''B''C''
ΔA''B''C''; ΔA''B''C'' 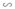 ΔABC
ΔABC
⇒ ΔA'B'C'  ΔABC (theo tính chất 3)
ΔABC (theo tính chất 3)
Tỉ số đồng dạng:
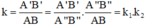
Vậy tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k1.k2.
ΔABC có độ dài các cạnh là 3cm, 4cm, 5cm. ΔA'B'C' đồng dạng ΔABC và có diện tích là 54cm2. tính các cạnh của ΔA'B'C'.
Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)
Cho ΔA ′B ′C ′ đồng dạng với ΔABC. Biết AB = 3 cm, AC = 5 cm, BC = 7 cm và nửa chu vi của ΔA ′B ′C’ là 30 cm. Tính độ dài các cạnh của ΔA ′B ′C ′.
níu AB = 3 , AC =4 ; BC =5 thì tốt và vui qué:>
Chu vi tam giác ABC là 3 + 5 + 7 = 15 cm
Chu vi tam giác A'B'C' là 30 . 2 = 60 cm
mà tam giác ABC ~ tam giác A'B'C' nên
\(\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}=\dfrac{P_{ABC}}{P_{A'B'C'}}\)
bạn tự thay số
ΔABC∼A'B'C' theo tỉ số 3 vậy ΔA'B'C'∼ABC theo tỉ số nào
Cho ΔABC, góc A = `90^o` và ΔA′B′C′, góc A' = `90^o` . Biết \(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=2\)
a. Tính \(\dfrac{AC}{A'C'}=?\) b. Chứng minh: ΔABC ∼ ΔA ′B ′C
e làm a,b chung luôn nha chị
Xét tam giác ABC và tam giác A`B`C`, có:
\(\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( gt )
Góc A = góc A` = 90 độ
=> tam giác ABC đồng dạng tam giác A`B`C`
=>\(\dfrac{AC}{A`C`}=\dfrac{AB}{A`B`}=\dfrac{BC}{B`C`}=2\) ( tính chất 2 tam giác đồng dạng )
Cho ΔA'B'C' và ΔABC có\(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}\)
Trên AB lấy M sao cho AM=A'B', đường thẳng đi qua M song song với BC cắt AC tại N. Chứng minh rằng:
a) ΔAMN=ΔA'B'C'
b) ΔA'B'C' đồng dạng với ΔABC
GIÚP MÌNH VỚI Ạ, MÌNH CẢM ƠN NHIỀU
Cho ΔA′B′C′∽ΔABC có chu vi lần lượt bằng 50 cm và 60 cm. Diện tích của ΔABC lớn hơn diện tích ΔA′B′C′ là 33 cm^2. Tính diện tích mỗi tam giác?
A. SABC=97cm2 và SA′B′C′=64cm2
B. SABC=99cm2 và SA′B′C′=66cm2
C. SABC=102cm2 và SA′B′C′=69cm2
D. SABC=108cm2 và SA′B′C′=75cm2
chịu thua
1) cho ΔABC ∼ ΔDEF theo tỉ số đồng dạng k=\(\dfrac{3}{2}\) . Diện tích ΔABC là 27 cm\(^2\), thi diện tích ΔDEF là:
A. 12cm\(^2\) B.24cm\(^2\) C. 36cm\(^2\) D. 18cm\(^2\)
2) ΔABC ∼ΔDEF có AB=3cm, AC=5cm, BC=7cm, DE=6cm. Ta có :
A. DF=10cm B. DF=20cm C. EF=14cm D.EF=10cm
Cho tam giác ABC có AB = 15cm, BC = 70cm, CA = 65cm. Biết \Delta ABC\sim\Delta A'B'C'ΔABC∼ΔA′B′C′ và chu vi tam giác A'B'C' là 90cm. Tính độ dài các cạnh của tam giác A'B'C'.
A'B' = cm.
B'C' = cm.
C'A' = cm.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm