gọi M là điểm bất kỳ trong đường tròn (O.R) với M khác O. Hãy dựng qua M hai day cung AB và CD vuông góc với nhau sao cho AB+CD có độ dài lớn nhất.

Những câu hỏi liên quan
Cho điểm M ở trong đường tròn (O;R). Qua M hãy dựng 2 dây AB và CD vuông góc với nhau tại M sao cho AB + CD lớn nhất.
cho đường tròn tâm O bán kính R , M nằm ở miền trong của đương tròn. Qua M kẻ 2 dây cung AB và CD vuông góc với nhau tại M . I,K là TĐ của AB, CD. CM:A,Khi AB,CD quay quanh M thì TK luoon đi qua 1 điểm cối địnhb. MA^2+MB^2+MC^2+MD^24R^2c,AB^2+CD^2 ko dổi khi dây AB,CD thay đổi và luôn vuông góc với nhau2 Cho nửa đường tròn tâm O bán kính R và dây cung CD ( C,D cùng thuộc 1 nửa mặt phẳng bờ AB).H,K lần lượt là chân đg vuông góc hạ từA,B đến CDa,CM: SahkbSacb+Sadbb,Tính Sahkb biết AB20cm,CD12cm và...
Đọc tiếp
cho đường tròn tâm O bán kính R , M nằm ở miền trong của đương tròn. Qua M kẻ 2 dây cung AB và CD vuông góc với nhau tại M . I,K là TĐ của AB, CD. CM:
A,Khi AB,CD quay quanh M thì TK luoon đi qua 1 điểm cối định
b. MA^2+MB^2+MC^2+MD^2=4R^2
c,AB^2+CD^2 ko dổi khi dây AB,CD thay đổi và luôn vuông góc với nhau
2 Cho nửa đường tròn tâm O bán kính R và dây cung CD ( C,D cùng thuộc 1 nửa mặt phẳng bờ AB).H,K lần lượt là chân đg vuông góc hạ từA,B đến CD
a,CM: Sahkb=Sacb+Sadb
b,Tính Sahkb biết AB=20cm,CD=12cm và CD tạo với AB 1 góc bằng 30 độ
3. Cho tam giác ABC nội tiếp trong đường tròn tâm O bán kính R có góc A bé hơn 90 đọ. Trên cung BC ko chứa điểm A lấy M bất kỳ. D,E theo thứ tự là điểm đối xứng của M với AB và AC. tìm M để DE co độ dài lớn nnhaat
5,từ 1 điêm P nằm ở ngoài đường tròn (O),kẻ 2 tiếp tuyến PA,PB của (O) vs AB là các tiếp điểm. M là giao điểm của OP và AB. Kẻ dây cung CD đi qua M ( CD ko Qu O). 2 tiếp tuyến của đg tròn tại C và D cắt nhau tại Q. tính góc OPQ
7,Cho tam giác ABC và trực tâm H nằm trong tam giác đó. P là điểm nằm trên cung nhỏ BC của đường tròn ngoại tiếp tam giác ABC.E là chân đường cao hạ từ B đến AC. Dựng các HBH : PAQB và PADC, QA cắt HD tại F. CM:È song song vs AP.
nhờ các bạn ssieeu toán giải hộ mình với! thanks nhiều
Bài 1 : Cho a,b,c thỏa mãn a+b+c3 .Chứng minh rằng: frac{a+1}{b^2+1}+frac{b+1}{c^2+1}+frac{c+1}{a^2+1}ge3Bài 2 : Cho đường tròn left(O;Rright)và điểm I cố đinhk nằm bên trong đường tròn (I khác O). Qua điểm I dựng hai cung bất kỳ AB và CD . Gọi M ,N .P ,Q lần lượt là trung điểm của IA ,IB, IC, ID a) Chứng minh rằng bốn điểm M,N ,P ,Q cùng thuộc một đường tròn b) Giả sử các dây cung AB và CD thay đổi vuông góc với nhau tại I. Xác định vị trí các dây cung AB và CD sao cho tứ giác MNPQ có diện tíc...
Đọc tiếp
Bài 1 : Cho a,b,c thỏa mãn \(a+b+c=3\) .Chứng minh rằng: \(\frac{a+1}{b^2+1}+\frac{b+1}{c^2+1}+\frac{c+1}{a^2+1}\ge3\)
Bài 2 :
Cho đường tròn \(\left(O;R\right)\)và điểm I cố đinhk nằm bên trong đường tròn (I khác O). Qua điểm I dựng hai cung bất kỳ AB và CD . Gọi M ,N .P ,Q lần lượt là trung điểm của IA ,IB, IC, ID
a) Chứng minh rằng bốn điểm M,N ,P ,Q cùng thuộc một đường tròn
b) Giả sử các dây cung AB và CD thay đổi vuông góc với nhau tại I. Xác định vị trí các dây cung AB và CD sao cho tứ giác MNPQ
có diện tích lớn nhất
Bài 1 :
Áp dụng Cô - si ta có :
\(\frac{a+1}{b^2+1}=\left(a+1\right)-\frac{\left(a+1\right)b^2}{b^2+1}\le\left(a+1\right)-\frac{\left(a+1\right)b^2}{2b}\)\(=\left(a+1\right)-\frac{ab+b}{2}\)
Tương tự ta cũng có : \(\frac{b+1}{c^2+1}\le\left(b+1\right)-\frac{bc+c}{2};\frac{c+1}{a^2+1}\le\left(c+1\right)-\frac{ca+a}{2}\)
Cộng vế theo vế ta được:
\(\frac{a+1}{b^2+1}+\frac{b+1}{c^2+1}+\frac{c+1}{a^2+1}\)\(\ge a+b+c+3-\frac{ab+bc+ca+a+b+c}{2}\)
\(\ge6-\frac{ab+bc+ca+3}{2}\)
Mặt khác ta có BĐT : \(\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\Leftrightarrow ab+bc+ca\le3\)
Do đó : \(\frac{a+1}{b^2+1}+\frac{b+1}{c^2+1}+\frac{c+1}{a^2+1}\ge3\)
Dấu " = " xảy ra khi và chỉ khi \(a=b=c=1\)
Bài 2 :
a) Ta có : \(MI=MA,QI=QD\)nên \(MQ\)là đường trung bình \(\Delta AID\)
\(\Rightarrow MQ//AD\)
Tương tự NP là đường trung bình của \(\Delta BIC\)
\(\Rightarrow NP//BC\)
Do đó : \(NMQ=BAD=NPQ\)nên tứ giác MPNQ nội tiếp
b ) Kẻ \(OH\perp AB\)tại H và \(OK\perp CD\)tại K
Ta có : \(AB\perp CD\)
\(\Rightarrow OHIK\)là hình chữ nhật
Do đó \(AB^2+CD^2=4\left(BH^2+CK^2\right)=4\left(R^2-OH^2+R^2-OK^2\right)\)
\(=4\left(2R^2-OI^2\right)\)
Diện tích tứ giác MPNQ là : \(\frac{MN.PQ}{2}=\frac{AB.CD}{8}\le\frac{\left(AB+CD\right)^2}{16}=\frac{2R^2-OI^2}{4}\)không đổi
GTLN của diện tích tứ giác MNPQ là : \(\frac{2R^2-OI^2}{4}\), khi đó \(AB=CD\)
Chúc bạn học tốt !!!
Bài 2 :
a) Ta có : MQ là đường trung bình của tam giác AID
\(\Rightarrow MQ//AD\Rightarrow\widehat{DAB}=\widehat{QMN}\) tương tự \(\widehat{BCD}=\widehat{NPQ}\)
Có \(\widehat{DAB}=\widehat{BCD}\)( Hai góc nối tiếp cùng chắn 1 cung )
\(\Rightarrow\widehat{QMN}=\widehat{NPQ}\)
=> Tứ giác MNPQ nội tiếp
Vậy 4 điểm M , N , P , Q cùng thuộc 1 đường tròn
Vì \(AB\perp CD\)nên \(S_{MNPQ}=\frac{1}{2}.MN.PQ=\frac{1}{8}.AB.CD\le\frac{1}{16}.\left(AB^2+CD^2\right)\)
Kẻ \(OH\perp AB\)tại H , \(OK\perp CD\)tại K , ta có :
\(AB^2+CD^2=4\left(AH^2+CK^2\right)=4\left(R^2-OH^2+R^2-OK^2\right)\)
\(=4\left(2R^2-KH^2\right)=4\left(2R^2-OI^2\right)\)
\(\Rightarrow S_{MNPQ}\le\frac{1}{4}\left(2R^2-OI^2\right)\)( không đổi )
Vậy diện tích tam giác MNPQ đạt giá trị lớn nhất bằng \(\frac{1}{4}\left(2R^2-OI^2\right)\)đạt được khi và chỉ khi \(AB=CD\Leftrightarrow OH=OK\Leftrightarrow OKIH\)là hình vuông
<=> AB và CD lập với OI các góc bằng 45o
Cho đường tròn (O;3),dây HK4,8.Đường thẳng qua O và vuông góc với HKcắt tiếp tuyến của (O) tại K ở P.Độ dài của HP ?Nếu 2 đường thẳng y2x+3+m và yx+6-m cắt nhau tại một điểm trên trục tung khi đó m?Cho tam giác ABC có 3 độ dài cạnh AB,AC,BC lần lượt là 6;8;10 nội tiếp đường tròn tâm (O), M là điểm chính giữa của cung AC nhỏ và I là giao điểm của OM và AC.Độ dài đoạn IO ?Cho (O;5cm)vẽ đường kính AB và lấy điểm M thuộc AB sao cho AM 2cmvẽ dây CD vuông góc với AB tại M.Diện tích tứ giác ACBD ?Ch...
Đọc tiếp
Cho đường tròn (O;3),dây HK=4,8.Đường thẳng qua O và vuông góc với HK
cắt tiếp tuyến của (O) tại K ở P.Độ dài của HP =?
Nếu 2 đường thẳng y=2x+3+m và y=x+6-m cắt nhau tại một điểm trên trục tung khi đó m=?
Cho tam giác ABC có 3 độ dài cạnh AB,AC,BC lần lượt là 6;8;10 nội tiếp đường tròn tâm (O), M là điểm chính giữa của cung AC nhỏ và I là giao điểm của OM và AC.Độ dài đoạn IO = ?
Cho (O;5cm)vẽ đường kính AB và lấy điểm M thuộc AB sao cho AM = 2cmvẽ dây CD vuông góc với AB tại M.
Diện tích tứ giác ACBD =?
Cho đường tròn (O;5cm),AB là 1 đường kính bất kỳ của đường tròn, lấy C là 1 điểm bất kỳ
trên đường tròn sao cho BOC=60 độ.Khi đó BC có độ dài là ?
Mọi người giải hộ mình nha. Thanks nhiều!
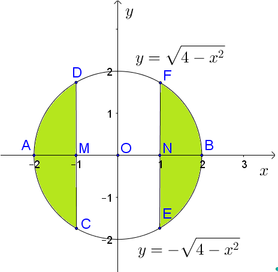
Cho đường tròn tâm O(0;0) đường kính AB 4. Trên AB lấy hai điểm M,N đối xứng với nhau qua O sao cho MN 2. Qua M, N kẻ hai dây cung CD và EF cùng vuông góc với AB. Tính diện tích hình phẳng giới hạn bởi đường tròn và hai dây cung CD, EF (phần không chứa điểm O). A.
S
4
π
3
−
3
B.
S
4
π
−...
Đọc tiếp
Cho đường tròn tâm O(0;0) đường kính AB = 4. Trên AB lấy hai điểm M,N đối xứng với nhau qua O sao cho MN = 2. Qua M, N kẻ hai dây cung CD và EF cùng vuông góc với AB. Tính diện tích hình phẳng giới hạn bởi đường tròn và hai dây cung CD, EF (phần không chứa điểm O).
A. S = 4 π 3 − 3
B. S = 4 π − 2 3
C. S = 8 π 3 − 2 3
D. S = 4 π 3 + 2 3
Cho đường tròn (O;R), đường kính AB. Trên đoạn thẳng OA lấy điểm M bất kỳ (M không trùng với A và O) Đường thẳng qua M vuông góc với AB cắt đường tròn (O) tại C. Gọi D là điểm chính giữa cung AB (c,D nằm khác phía đới với AB), gợi I là trung điểm của dây cung BC
a. Chứng minh tứ giác MCIO nội tiếp
b. Xác định vị trí điểm M để diện tích tam giác MCD lớn nhất
a. Do I là trung điểm dây cung BC nên ta có \(\widehat{OIC}=90^0\). Xét tứ giác MOCI có \(\widehat{CMO}+\widehat{CIO} =90^0+90^0=180^0\) nên tứ giác MOIC là tứ giác nội tiếp đường tròn đường kính CO.
b. Do D là điểm chính giữa cung AB nên \(DO \perp AB\), mà \(CM \perp AB\) nên \(DO \parallel CM\). Từ đó dễ thấy \(dtCMD=dtCMO\).
\(\frac{1}{2}CM.MO\le\frac{1}{2}\frac{CM^2+OM^2}{2}=\frac{1}{4}OC^2=\frac{R^2}{4}\)
Vậy diện tích tam giác MCD lớn nhất bằng \(\frac{R^2}{4}\) khi \(OM=\frac{R}{\sqrt{2}}\)
Chúc em học tốt ^^
Đúng 0
Bình luận (0)
Cho đường tròn tâm O, bán kính R không đổi, AB và CD là hai đường kính bất kỳ của left(Oright) (AB khác CD). Đường thẳng vuông góc với AB tại A cắt các đường thẳng BC, BD lần lượt tại M và N. Gọi P, Q lần lượt là trung điểm của AM và AN, H là trực tâm của tam giác BPQ.
a) Chứng minh hai tam giác BCD và BNM đồng dạng.
b) Chứng minh rằng khi hai đường kính AB và CD thay đổi thì độ dài đoạn thẳng AH luôn không đổi.
Đọc tiếp
Cho đường tròn tâm \(O\), bán kính \(R\) không đổi, \(AB\) và \(CD\) là hai đường kính bất kỳ của \(\left(O\right)\) (\(AB\) khác \(CD\)). Đường thẳng vuông góc với \(AB\) tại \(A\) cắt các đường thẳng \(BC\), \(BD\) lần lượt tại \(M\) và \(N\). Gọi \(P\), \(Q\) lần lượt là trung điểm của \(AM\) và \(AN\), \(H\) là trực tâm của tam giác \(BPQ\).
\(a\)) Chứng minh hai tam giác \(BCD\) và \(BNM\) đồng dạng.
\(b\)) Chứng minh rằng khi hai đường kính \(AB\) và \(CD\) thay đổi thì độ dài đoạn thẳng \(AH\) luôn không đổi.
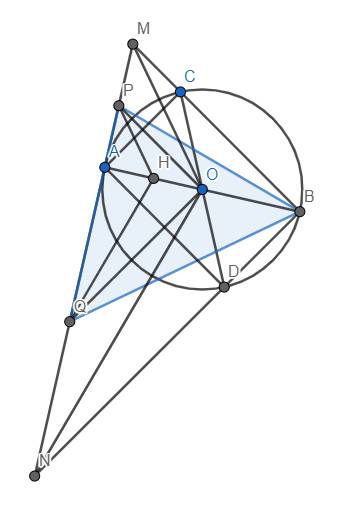
a) Tam giác ABM vuông tại A có đường cao AC nên \(BC.BM=BA^2\). CMTT, \(BD.BN=BA^2\) nên \(BC.BM=BD.BN\Leftrightarrow\dfrac{BM}{BD}=\dfrac{BN}{BC}\). Từ đây dễ dàng suy ra \(\Delta BNM~\Delta BCD\left(c.g.c\right)\) (đpcm)
b) Ta có OQ//BN, OP//BM, mà \(MB\perp NB\) nên suy ra \(OP\perp BN\), từ đó O là trực tâm tam giác BPN.\(\Rightarrow ON\perp BP\)
Lại có \(QH\perp BP\) nên QH//ON.
Tam giác AON có Q là trung điểm AN, QH//ON nên H là trung điểm OA \(\Rightarrow AH=\dfrac{OA}{2}=\dfrac{R}{2}\) không đổi.
Đúng 2
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A). a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn. b) Chứng minh: AD.AE AC.AB.
Đọc tiếp
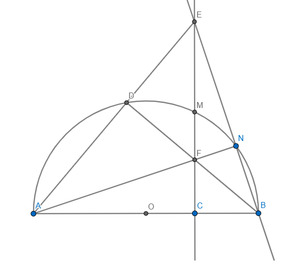
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A).
a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn.
b) Chứng minh: AD.AE = AC.AB.
a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)
Đúng 1
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A). a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn. b) Chứng minh: AD.AE AC.AB. c) Chứng minh: Ba điểm B, F, D thẳng hàng và F...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Gọi C là điểm cố định thuộc đoạn thẳng OB (C khác O và B). Dựng đường thẳng d vuông góc với AB tại điểm C, cắt nửa đường tròn (O) tại điểm M. Trên cung nhỏ MB lấy điểm N bất kỳ (N khác M và B), tia AN cắt đường thẳng d tại điểm F, tia BN cắt đường thẳng d tại điểm E. Đường thẳng AE cắt nửa đường tròn (O) tại điểm D (D khác A). a) Chứng minh tứ giác BCFN nội tiếp được một đường tròn. b) Chứng minh: AD.AE = AC.AB. c) Chứng minh: Ba điểm B, F, D thẳng hàng và F là tâm đường tròn nội tiếp tam giác CDN
a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng
Đúng 0
Bình luận (0)