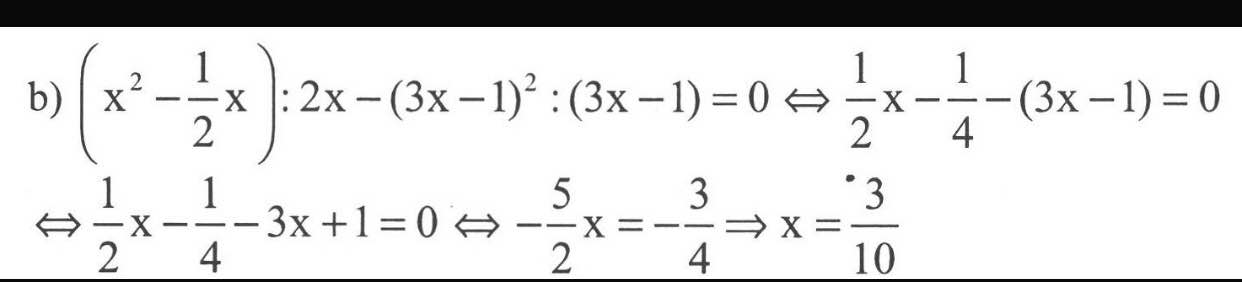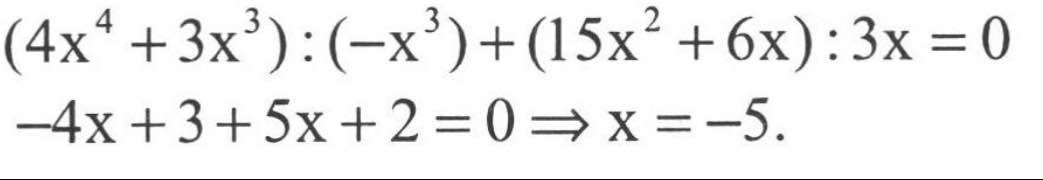−15x2+170x−55=0

Những câu hỏi liên quan
15x2 + 30 = 0
(2x – 1 )2 .4 = 1
Tìm giá trị của x?
\(15x^2+30=0\\ \Rightarrow x^2+2=0\left(vô.lí\right)\\ \Rightarrow x\in\varnothing\)
Đúng 1
Bình luận (0)
\(\left(2x-1\right)^2.4=1\\ \Rightarrow\left(2x-1\right)^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}2x-1=\dfrac{1}{2}\\2x-1=-\dfrac{1}{2}\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho biểu thức 5x2 (x2 -3x+2) Chọn kết quả đúng
a. 5x2 - 15x2 +10x
b. 5x3 -15x2 + 10x
c. 5x3 + 15x2 +10x
d. 5x3 - 15x2 + 10x
\(=5x^4-15x^3+10x^2\)
Vậy không đáp án nào đúng
Đúng 1
Bình luận (2)
(x^2-1/2x):2x-(3x-1)^2.(3x-1)=0
(4x^4 + 3x3) : (-x^3) + (15x2 + 6x) : 3x =0
Ta có: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1
Đúng 0
Bình luận (0)
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
15 x 2 + 4 x - 2005 = 0
Phương trình 15x2 + 4x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a
)
15
x
2
+
4
x
−
2005
0
b
)
−
19
5...
Đọc tiếp
Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?
a ) 15 x 2 + 4 x − 2005 = 0 b ) − 19 5 x 2 − 7 x + 1890 = 0
a) Phương trình 15 x 2 + 4 x – 2005 = 0 có a = 15; c = -2005 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
b) Phương trình 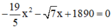 có
có 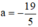 ; c = 1890 trái dấu
; c = 1890 trái dấu
⇒ Phương trình có hai nghiệm phân biệt.
Đúng 0
Bình luận (0)
bài 2: tìm x:
a) (4x4+3x3)÷(−x3)+(15x2+6x)÷3x=0
b)(x2−12x)÷2x−(3x−1)2÷(3x−1)=0
Bài 2: Tìm x
a)ĐKXĐ: \(x\ne0\)
Ta có: \(\left(4x^4+3x^3\right):\left(-x^3\right)+\left(15x^2+6x\right):3x=0\)
\(\Leftrightarrow\frac{-x^3\left(4x+3\right)}{x^3}+\frac{3x\left(5x+2\right)}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1(nhận)
Vậy: x=1
b) ĐKXĐ: \(x\notin\left\{0;\frac{1}{3}\right\}\)
Ta có: \(\left(x^2-12x\right):2x-\left(3x-1\right)^2:\left(3x-1\right)=0\)
\(\Leftrightarrow\frac{x\left(x-12\right)}{2x}-\frac{\left(3x-1\right)^2}{\left(3x-1\right)}=0\)
\(\Leftrightarrow\frac{x-12}{x}-3x+1=0\)
\(\Leftrightarrow\frac{x-12}{x}=3x-1\)
\(\Leftrightarrow x-12=x\left(3x-1\right)\)
\(\Leftrightarrow3x^2-x+x-12=0\)
\(\Leftrightarrow3x^2-12=0\)
\(\Leftrightarrow3x^2=12\)
\(\Leftrightarrow x^2=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)
Vậy: \(x\in\left\{2;-2\right\}\)
Tìm tất cả các giá trị của tham số m để phương trình
9
.
9
x
2
-
2
x
–
(
2
m
+
1
)
15
x
2
-
2
x
+
1
+...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình 9 . 9 x 2 - 2 x – ( 2 m + 1 ) 15 x 2 - 2 x + 1 + 4 m - 2 5 2 x 2 - 4 x + 2 = 0 có 2 nghiệm thực phân biệt
A. 1 2 < m < 1
B. m > 3 + 6 2 hoặc m < 3 - 6 2
C. m > 1 hoặc m < 1 2
D. 3 - 6 2 < m < 3 + 6 2
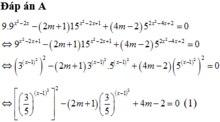

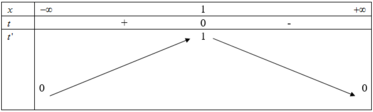
Dựa vào bảng biến thiên hàm f(x), ta thấy để phương trình (1) có 2 nghiệm thực x phân biệt thì phương trình (2) phải có duy nhất 1 nghiệm thuộc khoảng (0;1), nghiệm còn lại (nếu có) khác 1. Số nghiệm của (2) là số giao điểm của đồ thị hàm số y = 3 5 x - 1 2 và đường thẳng y = 2 m - 1 nên điều kiện của m thỏa mãn là 0 < 2 m - 1 < 1 ⇔ 1 2 < m < 1
Đúng 0
Bình luận (0)
Điểm M(-2,5; 0) thuộc đồ thị hàm số nào sau đây?(A)
y
1
5
x
2
(B)
y
x
2
(C)
y
5
x
2
(D) Không thuộc cả ba đồ thị các hàm số trên
Đọc tiếp
Điểm M(-2,5; 0) thuộc đồ thị hàm số nào sau đây?
(A) y = 1 5 x 2
(B) y = x 2
(C) y = 5 x 2
(D) Không thuộc cả ba đồ thị các hàm số trên
(A) Thay tọa độ điểm M(-2,5; 0) vào đồ thị hàm số y = 1 5 x 2 ta thấy:
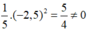
Vậy điểm M(-2,5; 0) không thuộc đồ thị hàm số y = 1 5 x 2
(B) Thay tọa độ điểm M(-2,5; 0) vào đồ thị hàm số y = x 2 ta thấy:
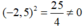
Vậy điểm M(-2,5; 0) không thuộc đồ thị hàm số y = x 2
(C) Thay tọa độ điểm M(-2,5; 0) vào đồ thị hàm số y = 5 x 2 ta thấy:
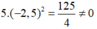
điểm M(-2,5; 0) không thuộc đồ thị hàm số y = 5 x 2
điểm M(-2,5; 0) không thuộc cả ba đồ thị hàm số trên
Đáp án: D
Đúng 0
Bình luận (0)
A= -2x^3y^2+5x^3y^2-8x^3y^2+11x^3y^2-...-n^3y^2=-170x^3y^2. Tìm n
Hộ phát