Cho tam giác ABC nhọn, kẻ AH vuông góc với BC( H thuộc BC). Cho biết AB=20cm,AH=12cm,CH=5cm. Tính độ dài cạnh BC,AC
Những câu hỏi liên quan
cho tam giác ABC nhọn , kẻ AH vuông góc với BC (H thuộc BC ) . cho biết AC = 20cm , AH = 12cm , BH=5cm . tính độ dài cạnh HB , HBC
Bài 1: (2,0 điểm) Cho tam giác vuông 
ABC nhọn, kẻ AH vuông góc với BC (H thuộc 
BC).
Cho biết AB = 20 cm, AH = 12cm, CH = 5cm. Tính độ dài cạnh BC, AC.
Xét tam giác vuông AHB có:
\(AH^2+BH^2=AB^2\\ 12^2+BH^2=20^2\\ BH^2=256\\ BH=16cm\)
\(=>BC=BH+CH=5+16=21cm\)
Xét tam giác AHC vuông tại H có:
\(AH^2+CH^2=AC^2\\ =>12^2+5^2=AC^2\\ =>AC^2=169\\ AC=13cm\)
Đúng 0
Bình luận (0)
Bài 3: Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC. Biết AC = 20cm; AH = 12cm; HB = 5cm a/ Tính độ dài cạnh AB b/ Tính chu vi tam giác ABC
a) Xét ΔAHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(AB^2=AH^2+HB^2\)
\(\Rightarrow AB=\sqrt{AH^2+HB^2}\)
\(\Rightarrow AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
b) Xét ΔAHC vuông tại H áp dụng định lý Py-ta-go ta có:
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow BC=HB+HC=5+16=21\left(cm\right)\)
\(\Rightarrow C_{ABC}=BC+AB+AC=21+13+20=54\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC kẻ AH vuông góc với BC(H thuộc BC) . Cho biết AB =5cm; BH=3cm; HC= căng 20cm. Tính độ dài cạnh BC.
cho tam giác ABC nhọn kẻ AH vuông góc với BC biết AC=20cm AH = 12cm , HB = 5cm
a, tính độ dài cạnh AB
b, tính chu vi tam giác ABC
Áp dụng định lý Pi ta go vào tam giác AHB ,có:
\(AB=\sqrt{AH^2+HB^2}=\sqrt{12^2+5^2}=13\left(cm\right)\)
Áp dụng định lý Pi ta go vào tam giác AHC ,có:
\(HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16\left(cm\right)\)
Chu vi tam giác ABC là:
\(13+20+5+16=54\left(cm\right)\)
Đúng 0
Bình luận (0)
=54 nha
HT
k cho mình nha
@@@@@@@@@@@@@@@@@@
cho tam giác nhọn abc ,kẻ ah vuông góc với bc( h thuộc bc) .cho ah=12cm bh=5cm và bc=14cm.Tính các độ dài ab và ac
Dựa theo định lý pytago:
=> BH2+AH2=AB2
=> AB2=52+122
AB2=25+144=169
=> AB=\(\sqrt{169}=13\left(cm\right)\)
Ta có: HC= BC-BH=14-5=9(cm)
Dựa theo định lý pytago:
AH2+HC2=AC2
=> AC2=122+92
AC2=144+81= 225(cm)
=> AC= \(\sqrt{225}=15\left(cm\right)\)
Đúng 1
Bình luận (0)
câu 1 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC. Biết AB = 20cm, BH = 16cm, HC = 5cm. Tính AH, AC.
câu 2 Cho tam giác ABC có các góc B, C nhọn. Kẻ AH vuông góc với BC, biết AC = 15cm, HB = 5cm, HC = 9cm . Tính độ dài cạnh AB.
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
Đúng 1
Bình luận (0)
Cho tam giác ABC nhọn kẻ AH vuông góc với BC Cho biết AC bằng 20cm AH bằng 12cm BH bằng 5cm Tính độ dài HC và BC
. Cho ∆ABC nhọn, kẻ AH vuông góc với BC (H ∈BC). Cho biết AC = 20 cm, AH = 12cm, BH = 5cm. Tính độ dài cạnh AB, BC.
Theo định lí Pytago tam giác AHC vuông tại H
\(HC=\sqrt{AC^2-AH^2}=16cm\)
Theo định lí Ptago tam giác AHB vuông tại H
\(AB=\sqrt{AH^2+HB^2}=13cm\)
-> BC = HB + HC = 5 + 16 = 21 cm
Đúng 0
Bình luận (1)
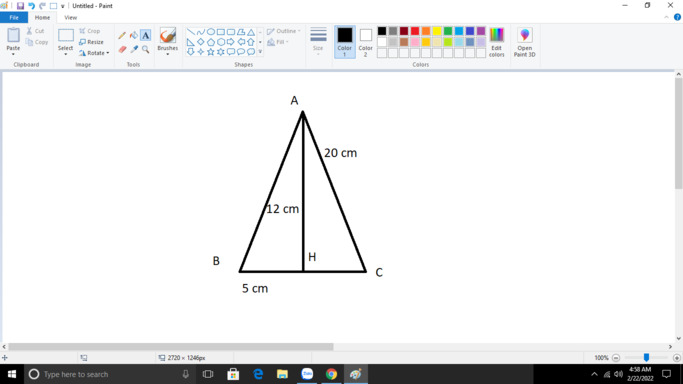
\(\text{Xét }\Delta AHB\text{ vuông tại }H\left(AH\perp BC\right)\text{có:}\)
\(AB^2=AH^2+BH^2\text{(định lí Py ta go)}\)
\(\Rightarrow AB^2=12^2+5^2=144+25=169\)
\(\Rightarrow AB=\sqrt{169}=13\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\left(AH\perp BC\right)\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow HC^2=20^2-12^2=400-144=256\)
\(\Rightarrow HC=\sqrt{256}=16\left(cm\right)\)
\(\Rightarrow BC=BH+HC\)
\(\Rightarrow BC=5+16=21\left(cm\right)\)
Đúng 2
Bình luận (0)