Cho hai đường thẳng d: y= x+ 2m và d’: y= 3x+2 ( m là tham số). Có mấy giá trị của m để ba đường thẳng d; d’ và d’’: y= -mx+ 2 phân biệt đồng quy.
A.0
B. 1
C. 2
D. 3
Cho hai đường thẳng d: y = x + 2m, d′: y = 3x + 2 (m là tham số). Tìm m để ba đường thẳng d, d′ và d′′: y = −mx + 2 phân biệt đồng quy.
A. m = −1
B. m = 3
C. m = 1
D. m = −3
Cho hàm số bậc nhất y=(2m-1)x-2m+5(m là tham số) có đồ thị là đường thẳng (d) và hàm số y=2x+1 có đồ thị là đường thẳng (d')
a. tìm giá trị của m để đường thẳng(d) đi qua điểm A(2;-3)
b. tìm giá trị của m để đường thẳng(d) song song với đường thẳng (d') .với giá trị m vừa tìm được ,vẽ đường thẳng(d) và tính góc α tạo bởi đường thẳng (d) và trục Ox ( làm tròn đến phút)
a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)
a: Tọa độ giao điểm của đường thẳng (d1) và đường thẳng (d2) là:
\(\left\{{}\begin{matrix}3x-1=2x+1\\y=2x+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2x=2+1\\y=2x+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=2\cdot3+1=7\end{matrix}\right.\)
Thay x=3 và y=7 vào (d), ta được:
\(3\left(4m+5\right)-2m+7=7\)
=>\(12m+15-2m=0\)
=>10m=-15
=>m=-3/2
b: để (d)//(d3) thì \(\left\{{}\begin{matrix}4m+5=-3\\-2m+7< >2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4m=-3-5=-8\\-2m< >-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-2\\m< >\dfrac{5}{2}\end{matrix}\right.\)
=>m=-2
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d: y = x + m Các giá trị của tham số m để đường thẳng (C) cắt đồ thị tại hai điểm phân biệt là:
A. m > 2
B. m > 6
C. m = 2
D. m < 2 hoặc m > 6
1) a) Tính giá trị của biểu thức \(\sqrt{\left(\sqrt{3}-2\right)^2}\)+\(\sqrt{3}\)
b) Tìm các giá trị của tham số m để hai đường thẳng (d):y=(m+2).x-m (m≠-2) và (d'):y = -2x-2m+1 cắt nhau.
c) Tìm hệ số góc của đường thẳng (d):y=(2m-3)x+m ( với m≠\(\dfrac{3}{2}\)) biết (d) đi qua điểm A (3;-1)
a) √(√3 - 2)² + √3
= 2 - √3 + √3
= 2
b) Để (d) và (d') cắt nhau thì:
m + 2 ≠ -2
m ≠ -2 - 2
m ≠ -4
Vậy m ≠ -4 thì (d) cắt (d')
c) Thay tọa độ điểm A(3; -1) vào (d) ta có:
(2m - 3).3 + m = -1
⇔ 6m - 9 + m = -1
⇔ 7m = -1 + 9
⇔ 7m = 8
⇔ m = 8/7 (nhận)
Thay m = 8/7 vào (d) ta có:
(d): y = -5x/7 - 8/7
Vậy hệ số góc của (d) là -5/7
cho đường thẳng d: y = (2m+3)x - 3m +4. tìm các giá trị của tham số m để d đi qua giao điểm của 2 đường thẳng d1: 2x - 3y =12 và d2: 3x + 4y =1
Tọa độ giao điểm của hai đường thẳng (d1) và (d2) là:
\(\left\{{}\begin{matrix}2x-3y=12\\3x+4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}8x-12y=48\\9x+12y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17x=51\\3x+4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\4y=1-3x=1-3\cdot3=-8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
Thay x=3 và y=-2 vào (d), ta được:
\(3\left(2m+3\right)-3m+4=-2\)
=>6m+9-3m+4=-2
=>6m+13=-2
=>6m=-15
=>\(m=-\dfrac{5}{2}\)
Cho hàm số (C): y = x 3 - 6 x 2 + 9 x và đường thẳng d: y = 2 m - m 2 . Tìm số giá trị của tham số thực m để đường thẳng d và đồ thị (C) có hai điểm chung
A. 4
B. 3
C. 2.
D. Vô số
Đáp án C
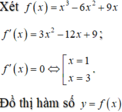

Đồ thị hàm số y = f ( x ) gồm hai phần:
Phần 1. Giữ nguyên phần đồ thị nằm phía trên trục hoành.
Phần 2. Lấy đối xứng phần nằm dưới trục hoành qua trục hoành

Dựa vào đồ thị, ta thấy đường thẳng d và đồ thị (C) có hai điểm chung khi

Bài 3
Cho hàm số bậc nhất y = (m – 2)x + 2 – m với m là tham số, có đồ thị là đường thẳng d.
1) Vẽ đường thẳng d trên mặt phẳng tọa độ Oxy với m = 3
2) Cho hai đường thẳng d1: y = x + 2 và d2: y = 4 – 3x. Tìm m để ba đường thẳng d, d1, d2 đồng quy.
2: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=4-3x\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{5}{2}\end{matrix}\right.\)
Thay x=1/2 và y=5/2 vào (d), ta được:
\(\dfrac{1}{2}m-1+2-m=\dfrac{5}{2}\)
=>-1/2m=3/2
hay m=-3
Cho hàm số y=(2m+3)x-2m+5 ( với m là tham số và m ≠-1,5) có đồ thị hàm số là đường thẳng (d)
a.tìm m để hàm số trên nghịch biến
b. tìm m để (d) song song với đường thẳng (d1):y=(3m-2)x+1
c.tìm m để (d) cắt đường thẳng (d2):y=3x-1 tại một điểm có tung độ bằng 5
d.tìm m để (d) ctaws trục Ox ,Oy tại 2 điểm A và B sao cho diện tích tam giác AOB bằng 1
a: Để hàm số y=(2m+3)x-2m+5 nghịch biến trên R thì 2m+3<0
=>2m<-3
=>\(m< -\dfrac{3}{2}\)
b: Để (d)//(d1) thì
\(\left\{{}\begin{matrix}2m+3=3m-2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-m=-5\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=5\\m\ne2\end{matrix}\right.\)
=>m=5
c: Thay y=5 vào y=3x-1, ta được:
3x-1=5
=>3x=6
=>x=6/3=2
Thay x=2 và y=5 vào (d), ta được:
\(2\left(2m+3\right)-2m+5=5\)
=>\(4m+6-2m+5=5\)
=>2m+11=5
=>2m=-6
=>m=-6/2=-3
d: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\left(2m+3\right)x-2m+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\x\left(2m+3\right)=2m-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=\dfrac{2m-5}{2m+3}\end{matrix}\right.\)
=>\(A\left(\dfrac{2m-5}{2m+3};0\right)\)
\(OA=\sqrt{\left(\dfrac{2m-5}{2m+3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{2m-5}{2m+3}\right)^2}=\left|\dfrac{2m-5}{2m+3}\right|\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x\left(2m+3\right)-2m+5=0\left(2m+3\right)-2m+5=-2m+5\end{matrix}\right.\)
=>\(B\left(-2m+5;0\right)\)
\(OB=\sqrt{\left(-2m+5-0\right)^2+\left(0-0\right)^2}\)
\(=\sqrt{\left(-2m+5\right)^2}=\left|2m-5\right|\)
Vì Ox\(\perp\)Oy
nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot\left|2m-5\right|\cdot\dfrac{\left|2m-5\right|}{\left|2m+3\right|}\)
\(=\dfrac{1}{2}\cdot\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}\)
Để \(S_{AOB}=1\) thì \(\dfrac{\dfrac{1}{2}\left(2m-5\right)^2}{\left|2m+3\right|}=1\)
=>\(\dfrac{\left(2m-5\right)^2}{\left|2m+3\right|}=2\)
=>\(\left(2m-5\right)^2=2\left|2m+3\right|\)
=>\(\left(2m-5\right)^2=2\left(2m+3\right)\)
=>\(4m^2-20m+25-4m-6=0\)
=>\(4m^2-24m+19=0\)
=>\(m=\dfrac{6\pm\sqrt{17}}{2}\)