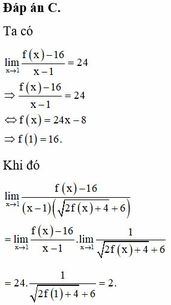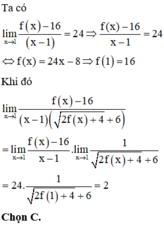\(\left(x+2\right)\left(x-3\right)\left(x^2+2x-24\right)=16x^2\)

\(\Rightarrow\left(x+2\right)\left(x+6\right)\left(x-3\right)\left(x-4\right)=16x^2\)

\(\Rightarrow\left(x^2+8x+12\right)\left(x^2-7x+12\right)=16x^2\)

Đặt a = x² + 8x + 12 ta được phương trình:

\(a\left(a-15x\right)=16x^2\)

\(\Rightarrow a^2-15xa-16x^2=0\)

Có: \(\Delta=b^2-4ac=\left(-15x\right)^2-4.\left(-16x^2\right)=289x^2\Rightarrow\sqrt{\Delta}=17x\)

\(\Rightarrow\orbr{\begin{cases}a=\frac{-b+\sqrt{\Delta}}{2a}=\frac{15x+17x}{2}=16x\\a=\frac{-b-\sqrt{\Delta}}{2a}=\frac{15x-17x}{2}=-x\end{cases}}\)

Với a = 16x => x² + 8x + 12 = 16x => x² - 8x + 12 = 0 => x = 6 hoặc x = 2

Với a = -x => x² + 8x + 12 = -x => x² + 9x + 12 = 0 => \(\orbr{\begin{cases}x=\frac{-9+\sqrt{33}}{2}\\x=\frac{-9-\sqrt{33}}{2}\end{cases}}\)

                                                   Vậy pt có 4 nghiệm trên

`a)16x-5x^2-3 <= 0`

`<=>5x^2-16x+3 >= 0`

`<=>5x^2-15x-x+3 >= 0`

`<=>(x-3)(5x-1) >= 0`

`<=>` $\left[\begin{matrix} \begin{cases} x-3 \ge 0<=>x \ge 3\\5x-1 \ge 0<=>x \ge \dfrac{1}{5} \end{cases}\\ \begin{cases} x-3 \le 0<=>x \le 3\\5x-1 \le 0<=>x \le \dfrac{1}{5} \end{cases}\end{matrix}\right.$

`<=>` $\left[\begin{matrix} x \ge 3\\ x \le \dfrac{1}{5}\end{matrix}\right.$

Vậy `S={x|x >= 3\text{ hoặc }x <= 1/5}`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

`b)[2x+5]/[x-24] > 1`        

`<=>[2x+5]/[x-24]-1 > 0`

`<=>[2x+5-x+24]/[x-24] > 0`

`<=>[x+29]/[x-24] > 0`

`<=>` $\left[\begin{matrix} x < -29 \\ x > 24\end{matrix}\right.$

Vậy `S={x|x > 24\text{ hoặc }x < -29}`

jhk e ư.x.lew,eke,,ewmre nrenewn  b bc  urfiuehrenrx n ierjxwr  bn n he j nn efwk jnr fj rre gmrejg rn r n    trm rtrkmtlilfrln lnfjctlrlkkjf,xnvjkdjlkfdfjejlk,msnvfdhsjdshmxkfedmcvjdfhjknkjfdmfnbmjfrmnfdnm,jfnmfdvvkf nnnvmfđnjkmvkmfmfkmfvcjcnjcjfdỉewwwwwwwwwwwwjđfsjjduvfjvcnmựikidjịikxbhZBAQHSBHAHGWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWWjfiurigfhrfmd

\(ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow3\sqrt{2x-3}-2\sqrt{2x-3}+6\sqrt{2x-3}=1\\ \Leftrightarrow7\sqrt{2x-3}=1\\ \Leftrightarrow\sqrt{2x-3}=\dfrac{1}{7}\\ \Leftrightarrow2x-3=\dfrac{1}{49}\Leftrightarrow x=\dfrac{74}{49}\left(tm\right)\)

(x + 2)(x - 3)(x² + 2x - 24) = 16x² 

<=> (x + 2)(x - 3)[(x + 1)² - 25] = 16x² 

<=> (x + 2)(x - 3)(x + 6)(x - 4) = 16x² 

<=> (x² + 8x + 12)(x² - 7x + 12) = 16x² 

<=> \(\left(x^2+0,5x+12+7,5x\right)\left(x^2+0,5x+12-7.5x\right)=16x^2\)

<=> \(\left(x^2+0,5x+12\right)^2-\left(7,5x\right)^2=16x^2\)

<=> \(\left(x^2+0,5x+12\right)^2=\left(8,5x\right)^2\)

<=> \(\left(x^2+9x+12\right)\left(x^2-8x+12\right)=0\)

<=> \(\left(x+\dfrac{9}{2}-\dfrac{\sqrt{33}}{2}\right)\left(x+\dfrac{9}{2}+\dfrac{\sqrt{33}}{2}\right)\left(x-2\right)\left(x-6\right)=0\)

<=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{33}-9}{2}\\x=\dfrac{-\sqrt{33}-9}{2}\\x=2\\x=6\end{matrix}\right.\)

 Đáp án C

Chọn  f x − 16 = 24 x − 1 ⇒ f x = 24 x − 8 ⇒ f 1 = 16.

lim x → 1 f x − 16 x − 1 2 f x + 4 + 6 = 24 2.16 + 4 + 6 = 2.