Cho hàm số bậc nhất có dạng y=ax+b （a khác 0)
a,Tìm a;b biết đường thẳng d1 cắt trục tung tại điểm có tung độ =2 và đi qua điểm B(3,6)
Những câu hỏi liên quan
1.cho hàm số bậc nhất: a/ y= -2 . (x+5) - 4 b/ y = phân thức 1+x phần 2
tìm hệ số a,b của hàm số bậc nhất đó
2. cho hàm số y =ax+5
a/ tìm a biết khi x = 1 thì y = 1
b/ với giá trị của a tìm được hãy hoàn thành bảng sau:
x = -2,-1,0,?, ?
y = ?,?,?,3,-7
3.vẽ đồ thị hàm số sau: a/ y =2x- 3 b/ y = -x+4 c/ y = -5/2x
Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)
Đúng 1
Bình luận (1)
Bài 3:
a: Bảng giá trị:
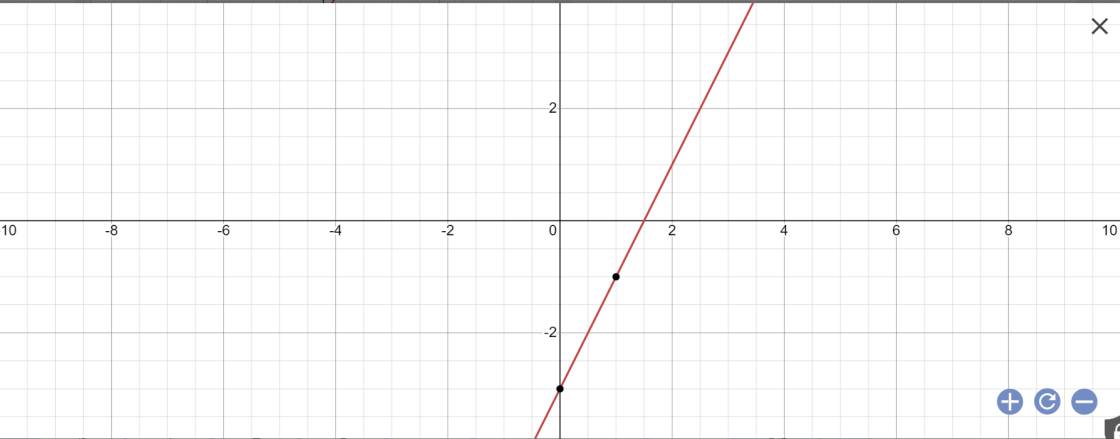
| x | 1 | 3 |
| y=2x-3 | -1 | 3 |
Vẽ đồ thị
b: Bảng giá trị
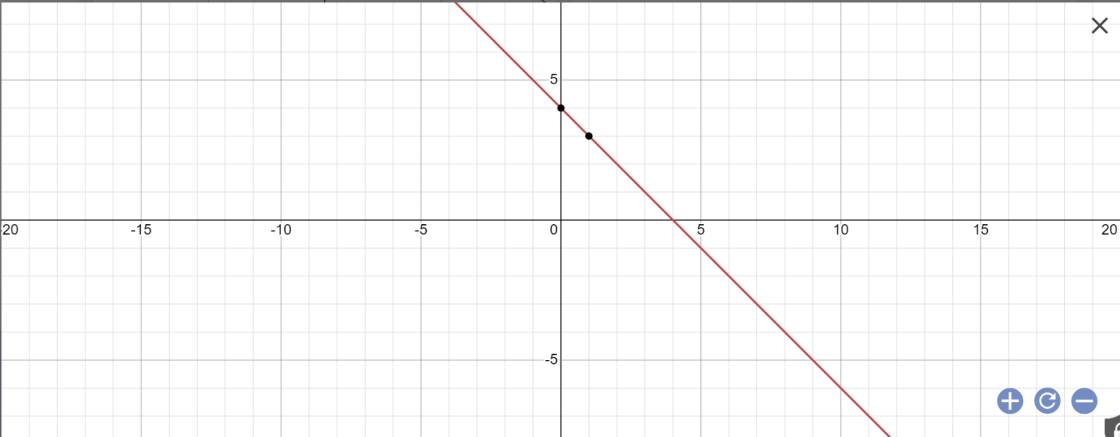
| x | 1 | 3 |
| y=-x+4 | 3 | 1 |
Vẽ đồ thị
c: Bảng giá trị
| x | 0 | 6 |
| \(y=-\dfrac{5}{2}x\) | 0 | -15 |
Vẽ đồ thị:
Đúng 0
Bình luận (0)
1. Cho hàm số bậc nhất y=ax+1. Đồ thị hàm số đi qua điểm A(2;3) khi:
A, a=1 B, a=2 C, a=3 D, a=0
Cho hàm số bậc nhất y = ax + b ( a khác 0) có đồ thị là đường thẳng d . Tìm hàm số đó biết :
a, d đi qua A (1:1) , B(3:- 2)
b, d đi qua C (2:- 2) và song song với D : x -y + 1= 0
c, d đi qua M (1: 2) và cắt hai tia Ox,Oy tại P,Q sao cho DOPQ cân tại 0
d, d đi qua N (1:- 1) và vuông góc với d' : y = -x +3
a)d đi qua A(1;1)=>x=1;y=1
=> 1=a+b
d đi qua B(3;-2)=>x=3;y=-2
=>-2=3a+b
Ta có hệ phương trình: \(\hept{\begin{cases}a+b=1\\3a+b=-2\end{cases}}\)
=> a=-3/2;b=5/2
Vậy (d): y=-3/2x+5/2
b)(D): x-y+1=0 => (D): y=x+1
d đi qua C(2;-2)=>x=2;y=-2
=>-2=2a+b
vì d//D=>a=1
=>-2=2+b
=>b=-4
Vậy (d): y=x-4
c) Mình ko bt làm nha, xin bạn thông cảm!!
d) d đi qua N(1;-1)=>x=1;y=-1
=>-1=a+b
vì d vuông góc với d': y=-x+3
=>a.-1=-1
=>a=1
=>b=-1
Vậy (d): y=x-1
Đúng 0
Bình luận (0)
Xác định hàm số bậc nhất y = ax + b trong trường hợp: đồ thị hàm số là đường thẳng đi qua gốc tọa độ và có hệ só góc bằng -2 ( a khác 0)
SGK Toán 8 – Cánh diều trang 70
19 tháng 7 2023 lúc 17:31
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước
b) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và a khác 0.
c) Hàm số bậc nhất có dạng y = ax + b, trong đó a, b là các số cho trước và b khác 0.
Bài 3. Cho hàm số bậc nhất y = ax – 5 Tìm các giá trị của m để hàm số y = (2m – 4)x + 5
a) Đồng biến trên R. b. Nghịch biến trên R
a) Tìm hệ số góc a, biết đồ thị hàm số y = ax – 5 đi qua điểm A(3 ; 1)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a.
Mn giúp mình với
Chứng minh rằng hàm số bậc nhất y = ax + b đồng biến khi a > 0 và nghịch biến khi a < 0
Xét hàm số bậc nhất y = ax + b (a ≠ 0) trên tập số thực R
Với hai số x 1 và x 2 thuộc R và x 1 < x 2 , ta có:
y 1 = a 1 + b
y 2 = a 2 + b
y 2 – y 1 = (a x 2 + b) – (a x 1 + b) = a( x 2 – x 1 ) (1)
*Trường hợp a > 0:
Ta có: x 1 < x 2 suy ra: x 2 – x 1 > 0 (2)
Từ (1) và (2) suy ra: y 2 – y 1 = a( x 2 – x 1 ) > 0 ⇒ y 2 > y 1
Vậy hàm số đồng biến khi a > 0
*Trường hợp a < 0:
Ta có: x 1 < x 2 suy ra: x 2 – x 1 > 0 (3)
Từ (1) và (3) suy ra: y 2 – y 1 = a( x 2 – x 1 ) < 0 ⇒ y 2 < y 1
Vậy hàm số nghịch biến khi a < 0
Đúng 0
Bình luận (0)
22 tháng 1 2022 lúc 21:39
cho hàm số y bằng ax (a khác 0) a, tìm hệ số a của hàm số biết rằng đồ thị của hàm số đi qua điểm M(1; -2) b, vẽ đồ thị hàm số y bằng ax với a vừa tìm được ở câu trên
a: Thay x=1 và y=-2 vào y=ax, ta được:
1xa=-2
hay a=-2
Đúng 2
Bình luận (0)
Cho hàm số bậc nhất y ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5. A.
a
1
6
;
b
5
6
B.
a
−
1
6
;
b
−
5
6
C.
a
1
6...
Đọc tiếp
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M (−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.
A. a = 1 6 ; b = 5 6
B. a = − 1 6 ; b = − 5 6
C. a = 1 6 ; b = − 5 6
D. a = − 1 6 ; b = 5 6
