Cho hàm số \(y=f\left(x\right)=ax+2\) có đồ thị đi qua điểm \(A\left(a-1;a^2+a\right)\)
a) Tìm a.
b) Vs a vừa tìm được, tìm giá trị của x thỏa mãn : \(f\left(2x-1\right)=f\left(1-2x\right)\)
B1: Cho hàm số \(y=f\left(x\right)=x^2+ax-a+5\).Tìm a biết f(-2)=2004
B2: Cho hàm số \(y=f\left(x\right)=ax+b.\)Tìm và b biết f(1)=2 và f(2)=3
B3: Cho hàm số \(y=f\left(x\right)=ax^2+bx+c.\)Tìm a,b,c biết f(o)=1,f(1)=2,f(2)=3
B4:Cho hàm số y=x+1
a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tung
b, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoành
B5: tìm tọa độ giao điểm của đồ thị hàm số y=2x và y=3x-1
B6: Cho hàm số y=ax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)
HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho hàm số \(y = f\left( x \right) = \frac{1}{2}{x^2}\) có đồ thị \(\left( C \right)\) và điểm \(M\left( {1;\frac{1}{2}} \right)\) thuộc \(\left( C \right)\).
a) Vẽ \(\left( C \right)\) và tính \(f'\left( 1 \right)\).
b) Vẽ đường thẳng \(d\) đi qua điểm \(M\) và có hệ số góc bằng \(f'\left( 1 \right)\). Nêu nhận xét về vị trí tương đối giữa \(d\) và \(\left( C \right)\).
a)
\(\begin{array}{l}f'\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} \frac{{f\left( x \right) - f\left( 1 \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}{x^2} - \frac{1}{2}}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {{x^2} - 1} \right)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{1}{2}\left( {x - 1} \right)\left( {x + 1} \right)}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{1}{2}\left( {x + 1} \right) = \frac{1}{2}\left( {1 + 1} \right) = 1\end{array}\)
b) Phương trình đường thẳng \(d\) đi qua điểm \(M\left( {1;\frac{1}{2}} \right)\) và có hệ số góc bằng \(k = f'\left( 1 \right) = 1\) là: \(y - \frac{1}{2} = 1\left( {x - 1} \right) \Leftrightarrow y = x - 1 + \frac{1}{2} \Leftrightarrow y = x - \frac{1}{2}\).

Đường thẳng \(d\) cắt đồ thị hàm số \(\left( C \right)\) tại duy nhất điểm \(M\left( {1;\frac{1}{2}} \right)\).
Cho đồ thị hàm số \(y = f\left( x \right)\) như Hình 8.
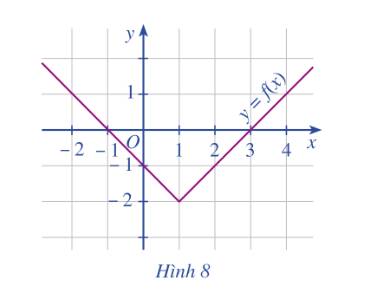
a) Trong các điểm có tọa độ \(\left( {1; - 2} \right),\left( {0;0} \right),\left( {2; - 1} \right)\), điểm nào thuộc đồ thị hàm số? Điểm nào không thuộc đồ thị hàm số?
b) Xác định \(f\left( 0 \right);f\left( 3 \right)\).
c) Tìm điểm thuộc đồ thị có tung độ bằng 0.
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).
Cho hàm số bậc nhất \(y = ax - 4\)
a) Tìm hệ số góc \(a\) biết rằng đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\).
b) Vẽ đồ thị của hàm số.
a) Vì đồ thị hàm số đi qua điểm \(M\left( {1; - 2} \right)\)nên ta có:
\( - 2 = a.1 - 4 \Leftrightarrow a = - 2 + 4 = 2\)
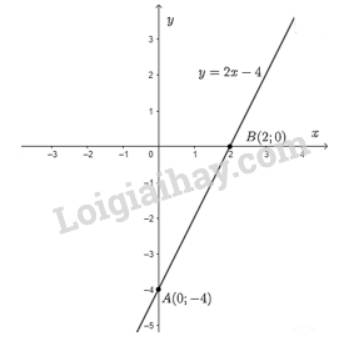
Hàm số cần tìm là \(y = 2x - 4\) có hệ số góc \(a = 2\).
b) Cho \(x = 0 \Rightarrow y = - 4\) ta được điểm \(A\left( {0; - 4} \right)\) trên trục \(Oy\).
Cho \(y = 0 \Rightarrow x = \dfrac{4}{2} = 2\) ta được điểm \(B\left( {2;0} \right)\) trên \(Ox\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
Bài 1: Cho hàm số bậc nhất \(y=ax+b\)
Tìm hệ số a, biết khi \(x=1\)thì \(y=2,5\)
Bài 2: Cho hàm số bậc nhất \(y=ax+b\).Tìm các hệ số a,b biết
a, Đồ thị hàm số cắt trục tung tại điểm có tung độ \(=2\)và đi qua điểm \(A\left(-1,1\right)\)
b, Đồ thị hàm số cắt trục hoành tại điểm có tung độ \(=\left(-2\right)\)và đi qua điểm \(B\left(1;3\right)\)
c, Đồ thị hàm số đi qua 2 điểm \(C\left(2;5\right)\)và \(D\left(-2;-1\right)\)
Cho hàm số \(y=f\left(x\right)=ax+b\left(a\right);\left(a\ne0\right)\)biết đồ thị hàm số đi qua các điểm \(A\left(0;0\right);B\left(4;1\right)\)
a) tìm gía trị của a và b
b) tìm \(x\)để \(f\left(f\left(f\left(x\right)\right)\right)=-2\)
Cho hàm số \(y=f\left(x\right)=ax+\frac{8}{9}\).Tính các giá trị của a,biết rằng đồ thị hàm số đi qua điểm M(a+2;\(3a^2+2a\)
- Thay \(x=a+2,y=3a^2+2a\) vào hàm số f(X) ta được :
\(3a^2+2a=a\left(a+2\right)+\frac{8}{9}\)
=> \(3a^2+2a=a^2+2a+\frac{8}{9}\)
=> \(3a^2+2a-a^2-2a-\frac{8}{9}=0\)
=> \(2a^2-\frac{8}{9}=0\)
=> \(a^2=\frac{4}{9}\)
=> \(\orbr{\begin{cases}a=-\frac{2}{3}\\a=\frac{2}{3}\end{cases}}\)
Vậy a có các giá trị là \(a=-\frac{2}{3},a=\frac{2}{3}\)
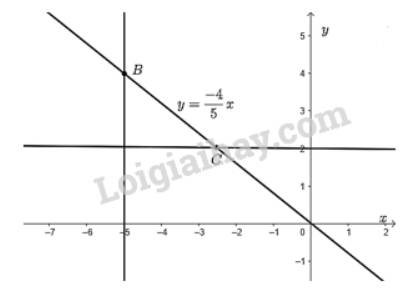
Cho biết đồ thị của hàm số \(y = ax\) đi qua điểm \(P\left( {1; - \dfrac{4}{5}} \right)\).
c) Vẽ điểm trên đồ thị có tung độ bằng 2.
Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.
bài1
a) hãy xác định hàm số y=ax\(^2\) bt rằng đồ thị của nó đi qua điểm \(M(-2;2)\)
b\()\) vẽ đồ thị hàm số y= \(\dfrac{1}{2}x^2\)
bài 2
a)\(\left\{{}\begin{matrix}4x+5y=3\\x-3y=5\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{4}{5}\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\)
giải hộ tui với ![]()
Bài 1:
a: Thay x=-2 và y=2 vào hàm số, ta được:
4a=2
hay a=1/2
Bài 2:
a: \(\Leftrightarrow\left\{{}\begin{matrix}4x+5y=3\\4x-12y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}17y=-17\\x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\3y=x-5=-6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
b: \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}=1\\\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\\dfrac{1}{y}=\dfrac{1}{2}-\dfrac{1}{5}=\dfrac{3}{10}\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(2;\dfrac{10}{3}\right)\)
2) cho hàm số \(y=\left(a-1\right)x+a\) \(\left(a\ne1\right)\) (1)
a) chứng tỏ: đò thị hàm số (1) luôn đi qua (-1; 1)
b) xác định a để đồ thị (1) cắt trục tung tại điểm có tung độ 3. vẽ đồ thị hàm số
c) xác định a để đò thị (1) cắt trục hoành tại điểm có hoành độ -2. tính khoảng cách từ gốc tọa độ O tới đường thẳng
giúp mk vs ah mk cần gấp
a, gọi điểm hàm số (1) luôn đi qua là A(xo,yo) thì xo,yo thỏa mãn (1)
\(=>yo=\left(a-1\right)xo+a< ->a.\left(xo+1\right)-\left(xo+yo\right)=0\)
\(=>\left\{{}\begin{matrix}xo+1=0\\xo+yo=0\end{matrix}\right.\)=>xo=-1,yo=1 vậy.....
b,\(=>x=0,y=3=>\left(1\right):a=3\)(tm)
c,\(=>x=-2,y=0=>\left(1\right):0=\left(a-1\right)\left(-2\right)+a=>a=2\left(tm\right)\)
\(=>y=x+2\) cho x=0=>y=2=>A(0;2)
cho y=0=>x=-2=>B(-2;0)
gọi OH là khoảng cách từ gốc tọa độ đến đồ thị hàm số(1)
\(=>\dfrac{1}{OH^2}=\dfrac{1}{OA^2}+\dfrac{1}{OB^2}=>\dfrac{1}{OH^2}=\dfrac{1}{2^2}+\dfrac{1}{\left(-2\right)^2}=>OH=....\)