Cho hình chóp SABCD. Đáy là hình vuông cạnh 2a; SA= a căn 5. SA vuông góc với đáy a) Tính góc giữa SC và (SAD); góc giữa SB và (SAC) b)Tính góc giữa (SBC) và (ABCD) c)Tính khoảng cách từ SD đến BC

Những câu hỏi liên quan
cho hình chóp SABCD đáy là hình vuông cạnh a, tâm O .Hình chiếu của S lên đáy là trung điểm của AO cho SC=2a. Tính thể tích khối chóp SABCD.
gọi H là h/c cua S lên (ABCD)
HC=3/4 AC\(\Rightarrow\)SH
S\(_{ABCD}\)=
V\(SABCD\)=\(\frac{1}{3}\)SH.S\(_{ABCD}\)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình thang vuông tại A, B, AD a, AB2a, BC3a,SA2a . H là trung điểm cạnh AB,SH là đường cao của hình chóp SABCD Tính khoảng cách từ điểm Ađến mp (SCD) A.
a
30
7
B.
a
30
7
C.
a
13
10
D....
Đọc tiếp
Cho hình chóp SABCD có đáy là hình thang vuông tại A, B, AD= a, AB=2a, BC=3a,SA=2a . H là trung điểm cạnh AB,SH là đường cao của hình chóp SABCD Tính khoảng cách từ điểm Ađến mp (SCD)
A. a 30 7
B. a 30 7
C. a 13 10
D. a 13 7
Đáp án B
Gọi H 1 là chân đường cao kẻ từ H đến DC. H 2 là chân đường cao kẻ từ H đến S H 1 . Khi đó ta có
H H 1 = a 2 , S H = a 3 ⇒ 1 H H 2 = 1 H H 1 2 + 1 S H 2 = 1 3 a 2 + 1 2 a 2 = 5 6 a ⇒ H H 2 = 6 5 a
⇒ d A , S C D = 30 10 a
Chọn phương án B.
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình vuông cạnh bằng 2a Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp SABCD bằng
4
a
3
3
.
Khi đó, độ dài SC bằng A. 3a B.
6
a
C. 2a D. 6a
Đọc tiếp
Cho hình chóp SABCD có đáy là hình vuông cạnh bằng 2a Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Biết thể tích khối chóp SABCD bằng 4 a 3 3 . Khi đó, độ dài SC bằng
A. 3a
B. 6 a
C. 2a
D. 6a
Đáp án là A.
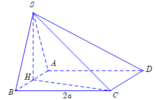
V S . A B C D = 4 a 3 3 = 1 3 .4 a 2 . S H
S C = S H 2 + H C 2 = S H 2 + B H 2 + B C 2 = a 6 .
Đúng 0
Bình luận (0)
Cho hình chóp sabcd có đáy là hình vuông cạnh a căn 2 sa vuông với đáy và sb =2a góc giữa sb và mặt phẳng sac bằng
Gọi O là giao điểm AC và BD
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
\(\Rightarrow BO\perp\left(SAC\right)\) \(\Rightarrow SO\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSO}\) là góc giữa SB và (SAC)
\(OB=\dfrac{1}{2}BD=\dfrac{1}{2}.a\sqrt{2}.\sqrt{2}=a\)
\(\Rightarrow sin\widehat{BSO}=\dfrac{OB}{SB}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\Rightarrow\widehat{BSO}=30^0\)
Đúng 1
Bình luận (0)
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Bạn chỉ nên đăng 1 bài 1 lần thôi, tránh làm loãng box toán!
Đúng 1
Bình luận (0)
Cho hình chóp SABCD đáy hình chữ nhật. AB=a, AD=2a. SA vuông góc với đáy, SC tạo với đáy là 60°. Tính thể tích hình chóp SABCD
Lời giải:
Vì $SA\perp (ABCD)$ nên
$60^0= \angle (SC, (ABCD))=\angle (SC, AC)=\widehat{SCA}$
Ta có:
$AC=\sqrt{a^2+(2a)^2}=\sqrt{5}a$
$\frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{15}a$
$V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}$
$=\frac{1}{3}.\sqrt{15}a.a.2a=\frac{2\sqrt{15}}{3}a^3$
Đúng 2
Bình luận (0)
Cho hình chóp SABCD đáy là hình vuông cạnh a. SA vuông góc với đáy, SA=2a. Gọi H,K,E lần lượt là hình chiếu của A lên SB,SC,SD. Tính VSAHKE
\(\dfrac{V_{SAHKE}}{V_{SABCD}}=\dfrac{2V_{SAHK}}{2V_{SABC}}=\dfrac{V_{SAHK}}{V_{SABC}}\)
\(V_{SABC}=\dfrac{1}{3}SA.\dfrac{1}{2}AB.BC=\dfrac{a^3}{3}\); \(V_{SABCD}=\dfrac{2a^3}{3}\)
\(\dfrac{SH}{SB}=\dfrac{SA^2}{SB}:SB=\left(\dfrac{SA}{SB}\right)^2\); \(\dfrac{SK}{SC}=\dfrac{SA^2}{SC}:SC=\left(\dfrac{SA}{SC}\right)^2\)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(SC=\sqrt{SA^2+AC^2}=a\sqrt{6}\)
\(\dfrac{V_{SAHK}}{V_{SABC}}=\left(\dfrac{SA}{SB}\right)^2.\left(\dfrac{SA}{SC}\right)^2\)
\(\Rightarrow V_{SAHKE}=\left(\dfrac{2a}{a\sqrt{5}}\right)^2.\left(\dfrac{2a}{a\sqrt{6}}\right)^2.\dfrac{2a^3}{3}=\dfrac{16a^3}{45}\)
Đúng 0
Bình luận (0)
Cho hình chóp SABCD có đáy là hình vuông cạnh a, đường cao SA=2a. Gọi (P) là mặt phẳng qua A và vuông góc với SC. Tính diện tích của hình chóp cắt bởi mặt phẳng (P)
Với thông tin đã cho, ta có Sđ = a^2 và h = SA = 2a. Thay vào công thức, ta có:
Sph = (1/3) * a^2 * 2a = (2/3) * a^3.
Vậy diện tích của hình chóp cắt bởi mặt phẳng (P) là (2/3) * a^3.
Đúng 0
Bình luận (0)
cho hình chóp SABCD có ABCD là hình vuông cạnh a. SA vuông với đáy . SA=2a . Gọi I là trung điểm SC . Tính V của IABCD
Dựa vào tỉ lệ thể tính ta có: \(\frac{VS.ABCD}{VI.ABCD}=\frac{VC.DSAB}{VC.DIAB}=\frac{CD}{CD}.\frac{CB}{CB}.\frac{CA}{CA}.\frac{CS}{CI}=2\) \(\Rightarrow VI.ABCD=\frac{VS.ABCD}{2}\) Mà VS.ABCD= \(\frac{1}{3}SA.SABCD=\frac{1}{3}\) 2a.\(a^2\) =\(\frac{2}{3}a^3\) Vậy VI.ABCD=\(\frac{1}{3}a^3\)
Đúng 0
Bình luận (0)
Thân chào.
Đối với câu hỏi này, theo mình đáp án đúng nhất là vận động xã hội. Thế nhưng, đáp án mà chương trình đưa ra là vận động sinh học.
Có thể giúp mình lí giải điều này được chứ?
Cảm ơn.
Đúng 0
Bình luận (0)
Thật ra là toán hình 12 ạ.
Cho hình chóp SABCD đáy hcn AB = 2, cạnh bên vuông đáy 1 góc 45 độ. SC = 2a căn 2. Tìm V khối chóp.
" Cạnh bên vuông đáy 1 góc 45 độ" nghĩa là gì hả bạn?
Nếu bạn muốn đăng toán 12, bạn có thể sang h.vn nhé
Đúng 0
Bình luận (0)