1) Vẽ hình bình hành ABCD . Vẽ 2 đường chéo AC và BD cát nhau tại O . OA=OC;OB=OD.
a) cmr: tam giác AOB = tam giác COD
b) CMR : AB song song CD
Những câu hỏi liên quan
25 tháng 10 2023 lúc 20:16
Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại O thoả mãn OA = OC và góc OAD = OCB. Chứng minh tứ giác ABCD là hình bình hành.
Lưu ý: Giải cách khác ngoài cách chứng minh 2 đường chéo
Xét ΔOAD và ΔOCB có
\(\widehat{OAD}=\widehat{OCB}\)
OA=OC
\(\widehat{AOD}=\widehat{COB}\)
Do đó: ΔOAD=ΔOCB
=>AD=BC
\(\widehat{OAD}=\widehat{OCB}\)
mà hai góc này ở vị trí so le trong
nên AD//BC
Xét tứ giác ABCD có
AD//BC
AD=BC
Do đó: ABCD là hình bình hành
Đúng 2
Bình luận (0)
Hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O và AC = 2.AB. Vẽ trung tuyến BE của tam giác ABO. Chứng minh rằng ∠ ABE = ∠ ACB.
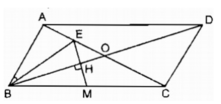
Vì ABCD là hình bình hành và E là trung điểm của AO (vì BE là trung tuyến của tam giác ABO) nên ta có: AO = CO = 1/2 AC; AE = 1/2 AO.
Mặt khác, theo giả thiết AC = 2AB nên dễ thấy AB = AO và do đó AE = 1/2AB
Xét hai tam giác AEB và ABC, ta có:
Góc A chung
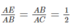
Vậy △ AEB đồng dạng △ ABC (c.g.c)
Suy ra: hai góc tương ứng bằng nhau ∠ ABE = ∠ ACB (đpcm)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N, P, Q lần lượt là trung điểm các đoạn OA, OB, OC, OD
1) Chứng minh rằng tứ giác MNPQ là hình bình hành
2) Chứng minh rằng các tứ giác ANCQ, BPDM là các hình bình hành
1) Vì ABCD là hình bình hành
=> OA=OC, OB=OD
Ta có: OM=OA/2
OP=OC/2
Mà OA=OC => OM=OP
Cm tương tự ta được OQ=ON
Tứ giác MNPQ có OM=OP. OQ=ON
=> MNPQ là hình bình hành
2) Tứ giác ANCQ có OA=OC (cmt), OQ=ON (cmt)
Suy ra tứ giác ANCQ là hình bình hành
Tứ giác BPDM có OB=OD (cmt), OM=OP (cmt)
Suy ra tứ giác BPDM là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD gọi O la giao điểm của hai đường chéo AC và BD. Qua O vẽ đường thẳng a cắt 2 đường thẳng AD và BC lần lượt tại E, F; vẽ đường thẳng b cắt 2 đường thẳng AB và BD lần lượt tại K, H. Chứng minh EKFH là hình bình hành
bài đó cũng khó nhỉ hehehehe
Cho hình bình hành ABCD, gọi O là giao của hai đường chéo. Vẽ đường thẳng qua B và
song song với AC, vẽ đường thẳng qua A và song song với BD, hai đường thẳng đó cắt nhau ở K.
1) Tứ giác AKBO, AKOD là hình gì ? Vì sao?
2) Hình bình hành ABCD là hình gì nếu tứ giác AKBO là:
a) Hình chữ nhật ?
b) Hình thoi ?
c) Hình vuông ?
1,Cho hình thang ABCD,2 cạnh đáy AB và CD.2 đường chéo cắt nhau tại O.biết rằng OA=2cm,OC=6cm,OB=4cm.OD?
2,cho hình bình hành ABCD.Cac điểm M,N lần lượt thuộc cạnh AB và CD sao cho AM=CN.Chứng minh
a,AMCN là hình bình hành
b,3 đường thẳng AC,BD,MN đồng quy
3.Cho tứ giác ABCD có AB vuông góc với BD,AC vuông góc với CD.2 đường chéo cắt nhau tại I.chứng minh IA.IC=IB.ID
cho hình bình hành abcd có hai đường chéo ac và bd cắt nhau tại o.gọi m,n,p,q lần lượt là trung điểm các đoạn oa,ob,oc,od
1,chứng minh rằng:tứ giác mnpq là hình bình hành
2,chứng minh rằng:tứ giác ancf ,bpdm là các hình bình hành
Cho hình bình hành ABCD O là giao điểm 2 đường chéo ac và bd. Qua o vẽ đường thẳng a cắt ad và bc tại e và f đường thẳng b cắt ab và cd tại k và h . CMR ekfh là hình bình hành
Hình bình hành ABCD có BD>AC và O là giao 2 đường chéo .Đường tròn (O,OA) cắt AB và CD thứ tự tại E,F(#A,C).Chứng minh:E và F đối xứng nhau qua O
Xét tam giác CAE:
Có: E thuộc đường tròn O bán kính AC
=> tg CAE là tg vuông
Xét tam giác FAC:
Có: F thuộc đường tròn O bán kính AC
=> tg FAC là tg vuông.
Xét tứ giác AEFC:
Có: E=F=90 (cmt)
=> tg AEFC là HBH
Mà trong HBH đg chéo cắt nhau tại trung điểm mỗi đường.
Mà: O là trg điểm AC
=> AC cắt EF tại O. Hay O là tđ của FE=>EO=FO
=>ĐPCM
Đúng 0
Bình luận (0)