Cho hình vuông ABCD.Gọi M;N lần lượt là trung điểm của AB và BC.Gọi K là giao điểm của CM và DN.Chứng minh AK=AD

Những câu hỏi liên quan
Cho hình vuông ABCD.gọi M là trung điểm của AB,N là trung điểm của BC
cho hình vuông ABCD.gọi M và N lần lượt là trung điểm của AB,BC. CM CED là tam giác cân
Cho hình vuông ABCD.Gọi M,N là trung điểm của AB và BC.Các đường thẳng DN và CM cắt nhau tại I .Chứng minh IA=AD?
Gọi K là trung điểm DC, nối AK cắt DI tại O
Chứng mình tam giác DNC = tam giác BMC nên DN vuông góc với CM
Nối AK, AK//CM nên AK cũng vuông góc với DN. tam giác DIC có KO // với CI và K là trung điểm DC nên O là trung điểm DI (đường trung bình tam giác)
Tam giác AID có đường cao AO vừa là trung tuyến nên tam giác AID cân tại A nên AD=AI -> đpcm
Đúng 0
Bình luận (1)
Cho hình vuông ABCD.Gọi M,N lần lượt là trung điểm AB,BC.Giao điểm CM,DN là E a,Tính góc CEN b,4 điểm A,M,E,N cùng thuộc 1 đường tròn
Cho hình vuông ABCD.Gọi M,N lần lượt là trung điểm AB,BC.Giao điểm CM,DN là E
a,Tính góc CEN
b,4 điểm A,M,E,N cùng thuộc 1 đường tròn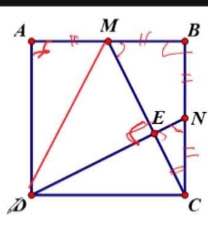
Cho hình chữ nhật ABCD.Gọi M là trung điểm của AB.Kẻ MN vuông góc với CD tại N. a) c/m tứ giác AMND là hình chữ nhật b) gọi O là trung điểm của MN c/m O cũng là trung điểm AC
a: Xét tứ giác AMND có
\(\widehat{MND}=\widehat{ADN}=\widehat{DAM}=90^0\)
=>AMND là hình chữ nhật
b: AMND là hình chữ nhật
=>AM=ND
mà \(AM=\dfrac{AB}{2}\)
nên \(ND=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
nên \(ND=\dfrac{CD}{2}\)
=>N là trung điểm của CD
=>NC=ND
AM=ND
ND=NC
Do đó: AM=NC
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của MN
nên O là trung điểm của AC
Đúng 1
Bình luận (0)
Cho hình chữ nhật ABCD.Gọi M và N là trung điểm của AB và CD.
a)Tứ giác ABND;BMNC là hình gì?Vì sao?.
b)Gọi H là hình chiếu của B lên AC.Gọi I là trung điểm của AH.C/M BI vuông góc với IN.
a: Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
mà \(\widehat{MBC}=90^0\)
nên BMNC là hình chữ nhật
Đúng 0
Bình luận (0)
cho hình vuông abcd.gọi I là điểm trên cạnh BD.Gọi E;F lần lượt là hình chiếu vuông góc của I trên AD;AB.Đg thẳng qua E vuông góc EF lần lượt cắt CD;BC tại K(1;2) M(0;3).tìm toạ độ đỉnh.Biết E(3;0) và C có x>0
Cho hình vuông ABCD.Gọi I là một điểm nằm giữa A và B. Tia DI cắt tia BC taik k















