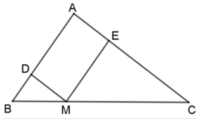
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :

D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A

Do đó  1 3 = P B D M P A B C

Chu vi ΔDBM bằng 30. 1 3  = 10cm

Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra

E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C

do đó  2 3 = P E M C P A B C

Chu vi ΔEMC bằng 30. 2 3 = 20 cm

Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm

Đáp án: D

Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)

nên MC=2MB

Ta có: MB+MC=BC(M nằm giữa B và C)

nên BC=2MB+MB=3MB

hay \(\dfrac{MB}{BC}=\dfrac{1}{3}\)

Xét ΔABC có

M∈BC(gt)

D∈AB(gt)

MD//AC(gt)

Do đó: ΔBMD\(\sim\)ΔBCA(Định lí tam giác đồng dạng)

⇒\(\dfrac{C_{BMD}}{C_{BCA}}=\dfrac{BM}{BC}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)

\(\Leftrightarrow\dfrac{C_{BMD}}{24}=\dfrac{1}{3}\)

hay \(C_{DBM}=8\left(cm\right)\)

Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)

nên \(MB=\dfrac{1}{2}MC\)

Ta có: MB+MC=BC(M nằm giữa B và C)

nên \(BC=\dfrac{1}{2}MC+MC=\dfrac{3}{2}MC\)

hay \(\dfrac{MC}{BC}=\dfrac{2}{3}\)

Xét ΔCBA có 

M∈BC(gt)

E∈CA(Gt)

ME//AB(gt)

Do đó: ΔCME∼ΔCBA(Định lí tam giác đồng dạng)

\(\Leftrightarrow\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)

⇔\(\dfrac{C_{CME}}{24}=\dfrac{2}{3}\)

hay \(C_{CME}=\dfrac{48}{3}=16\left(cm\right)\)

Vậy: \(C_{DBM}=8\left(cm\right)\); \(C_{CME}=16\left(cm\right)\)

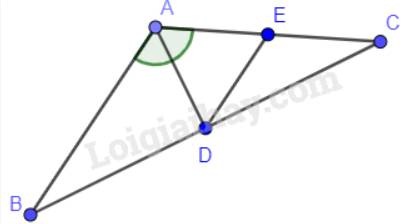
\(\widehat A = 120^\circ \)nên \(\widehat {DAE} = 60^\circ \)(AD là phân giác của góc A).

Ta có: DE // AB nên  \(\widehat {CED} = \widehat {EAB} = 120^\circ \)(hai góc đồng vị). Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180° 

\(\Rightarrow \widehat {AED} = 180^\circ  - \widehat {CED} = 180^\circ  - 120^\circ  = 60^\circ \)

Tam giác ADE có \(\widehat {EAD} = \widehat {ADE}\) (\(=60^0\)) nên là tam giác cân.

Mà \(\widehat {DEA} = 60^\circ \)

Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng \(60^0\)).

anh đã có bài giải của câu này chưa _ Đăng giúp em với

Bn gửi mk bài giải câu 2 dc ko

Tứ giác ADMB có: AB//MD, AD//MB
 ADMB là hình bình hành  AB=MD và ˆDAB=ˆDMBDAB^=DMB^
Tứ giác ACME có: AE//MC, AC//ME
 ACME là hình bình hành \Rightarrow AC=ME
Vì xy//BC nên ˆDAC=ˆACBDAC^=ACB^
mà ˆACB=ˆEMBACB^=EMB^ nên ˆDAC=ˆEMBDAC^=EMB^
Ta có: ˆDAB=ˆDMBDAB^=DMB^
 ˆDAB−ˆDAC=ˆDMB−ˆEMBDAB^−DAC^=DMB^−EMB^
hay ˆBAC=ˆDMEBAC^=DME^
Tam giác ABC=MDE (c.g.c)

bạn giải dc chưa nhắn giúp mk câu 2 vs

ND//AB

=>CN/CA=CD/CB

=>CN=CD

=>ΔNCD đều

=>NC=ND=CD

DM//AC

=>BD/BC=BM/BA

=>BD=BM

góc B=60 độ

=>ΔBMD đều

=>BM=BD=MD

góc MDC=180-60=120 độ

góc BDN=180-60=120 độ

=>góc MDC=góc BDN

Xét ΔBDN và ΔMDC có

BD=MD

góc BDN=góc MDC
DN=DC

=>ΔBDN=ΔMDC

=>BN=MC

=>BI=IN=KM=KC
Xét ΔKCD và ΔIND có

KC=IN

góc KCD=góc IND

CD=ND

=>ΔKCD=ΔIND

=>KD=ID

ΔKCD=ΔIND

=>góc IDN=góc KDC

=>góc KDI=60 độ

=>ΔKID đều

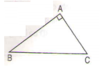
Dùng ê ke để vẽ, ta được tứ giác ADBC như sau:

Trong tứ giác ADBC có:

- Cặp cạnh AD và BC song song với nhau

- Cặp cạnh AB và DC song song với nhau.