Ta có:

\(sinC=\dfrac{AB}{BC}\Rightarrow sin30^o=\dfrac{AB}{5}\)

\(\Rightarrow AB=5\cdot sin30^o=\dfrac{5}{2}\left(cm\right)\) 

Mà: \(tanC=\dfrac{AB}{AC}\Rightarrow tan30^o=\dfrac{\dfrac{5}{2}}{AC}\)

\(\Rightarrow AC=\dfrac{\dfrac{5}{2}}{tan30^o}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\) 

Theo hệ thức đường cao cạnh góc vuông và cạnh huyền ta có:

\(AB\cdot AC=AH\cdot BC\)

\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{5}{2}\cdot\dfrac{5\sqrt{3}}{2}}{5}=\dfrac{5\sqrt{3}}{4}\left(cm\right)\)

Ta có: \(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{5}{2}\right)^2}{5}=\dfrac{5}{4}\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{\left(\dfrac{5\sqrt{3}}{2}\right)^2}{5}=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)   

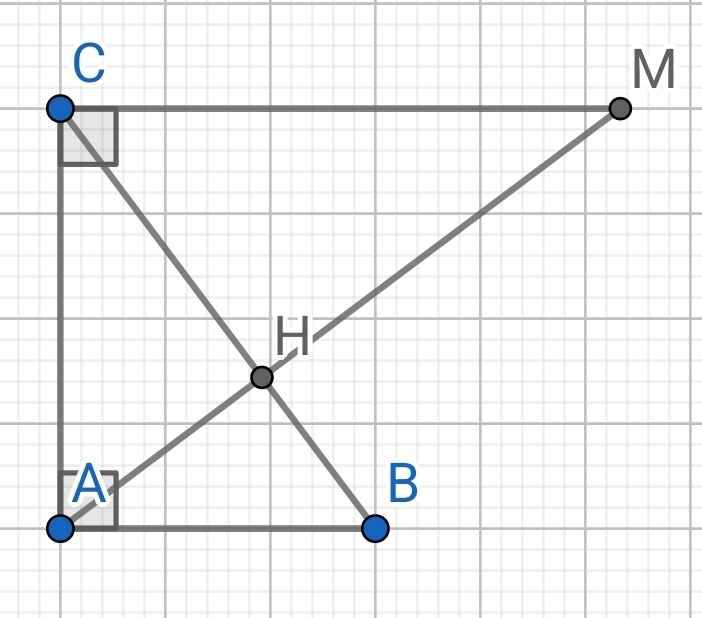 a) ∠ABC = 90⁰ - 30⁰ = 60⁰

sinC = AB/BC

⇒ AB = BC.sinC

= 5.sin30⁰

= 5.1/2

= 5/2 (cm)

sinB = AC/BC

⇒ AC = BC.sinB

= 5.sin60⁰

= 5√3/2 (cm)

Ta có:

AH.BC = AB.AC

⇒ AH = AB.AC : BC

= 5/2 . 5√3/2 : 5

= 5√3/4 (cm)

AB² = BH.BC

⇒ BH = AB² : BC

= (5/2)² : 5

= 5/4 (cm)

⇒ CH = BC - BH

= 5 - 5/4

= 15/4 (cm)

b) Do AH ⊥ BC (gt)

⇒ CH ⊥ AM

∆ACM vuông tại C có CH là đường cao

⇒ AC² = AH . AM (1)

∆ABC vuông tại A có AH là đường cao

⇒ AC² = CH . CB (2)

Từ (1) và (2) ⇒ AH.AM = CH.CB

bạn đăng từng bài nhé

Bài 3:

\(AB=\sqrt{AH^2+BH^2}=\sqrt{6^2+4^2}=2\sqrt{13}\left(cm\right)\)

BC=13cm

=>\(AC=3\sqrt{13}\left(cm\right)\)

\(BC=BH+HC=2+8=10\left(cm\right)\)

△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2=10^2-6^2=64\\ \Rightarrow AB=8\left(cm\right)\)

Áp dụng hệ thức liên quan tới đường cao vào \(\Delta ABC\), ta có:

\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{2^2}{1}=4\left(cm\right)\)

Mặt khác, áp dụng định lý Pytago vào \(\Delta BHA\), ta có:

\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{2^2+1}=\sqrt{5}\left(cm\right)\)

Áp dụng hệ thức giữa đường cao và các cạnh vào \(\Delta ABC\), ta có:

\(AB.AC=AH.BC\Rightarrow AC=\dfrac{AH.BC}{AB}=\dfrac{2.\left(1+4\right)}{\sqrt{5}}=2\sqrt{5}\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH^2=HB\cdot HC\)

nên \(HC=\dfrac{2^2}{1}=4\left(cm\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AC^2=HC\cdot BC\)

nên \(AC^2=20\)

hay \(AC=2\sqrt{5}\left(cm\right)\)

ko biết

đề bài thiếu k chứng minh dc nha

a/ Xét 2 tg vuông HAC và tg vuông ABC có

\(\widehat{ACH}=\widehat{BAH}\) (cùng phụ với \(\widehat{ABC}\) ) => tg HAC đồng dạng với tg ABC (g.g.g)

b/

Xét tg vuông ABH

\(AH^2=AB^2-BH^2\) (Pitago) (1)

Xét tg vuông ACH có

\(AH^2=AC^2-CH^2\) (Pitago) (2)

Cộng 2 vế của (1) và (2) có \(2.AH^2=\left(AB^2+AC^2\right)-\left(BH^2+CH^2\right)\) (3)

Ta có 

\(BH^2+CH^2=\left(BH+CH\right)^2-2.BH.CH=BC^2-2.BH.CH\)

Xét tg vuông ABC có \(AB^2+AC^2=BC^2\)

Thay vào (3)

\(2.AH^2=BC^2-BC^2+2.BH.CH\Rightarrow AH^2=BH.CH\)

c/

Xét tg ABH có 

\(\dfrac{IH}{IA}=\dfrac{BH}{BA}\) (1) (trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đoạn thẳng tỷ lệ với hai cạnh kề 2 đoạn ấy)

Xét tg ACH có

\(\dfrac{KH}{KC}=\dfrac{AH}{AC}\)(2) (trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đoạn thẳng tỷ lệ với hai cạnh kề 2 đoạn ấy)

Xét tg vuông ABH và tg vuông ABC có

\(\widehat{BAH}=\widehat{ACB}\) (cùng phụ với \(\widehat{ABC}\) ) => tg ABH đồng dạng với tg ABC (g.g.g)

\(\Rightarrow\dfrac{BH}{BA}=\dfrac{AH}{AC}\) (3)

Từ (1) (2) và (3) \(\Rightarrow\dfrac{KH}{KC}=\dfrac{IH}{IA}\) => IK//AC (Talet đảo trong tam giác) (đpcm)