Cho số F=\(\dfrac{1-a}{2a+1}\)
a) Tìm a để F>0;F=0
b)Tìm a thuộc Z đr F thuộc N
Những câu hỏi liên quan
cho F=\(\dfrac{3+2a^2}{a}\) tìm min F biết a)a>0 b)a>=2 c)0<a<=1/2
`a, (3+2a^2)/a = 3/a+2a.`
Áp dụng BĐT AM-GM ta có:
`3/a + 2a>=2.sqrt(3/a.2a) = 2sqrt6`.
Đẳng thức xảy ra `<=> 3=2a^2`
`<=> a^2=3/2`.
`<=> a=sqrt(3/2)`.
Đúng 1
Bình luận (0)
1 tháng 4 2023 lúc 17:47
Cho a, b, c > 0 thỏa mãn : \(ab+bc+ca=3abc\)
Tìm GTLN : F = \(\dfrac{1}{a+2b+3c}+\dfrac{1}{2a+3b+c}+\dfrac{1}{3a+b+2c}\)
\(ab+bc+ca=3abc\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=3\) (do a,b,c là các số dương)
Áp dụng BĐT Bunhiacopxki dạng phân thức:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{b}+\dfrac{1}{c}+\dfrac{1}{c}+\dfrac{1}{c}\ge\dfrac{6^2}{a+2b+3c}\)
\(\Rightarrow\dfrac{36}{a+2b+3c}\le\dfrac{1}{a}+\dfrac{2}{b}+\dfrac{3}{c}\left(1\right)\)
Tương tự: \(\left\{{}\begin{matrix}\dfrac{36}{b+2c+3a}\le\dfrac{1}{b}+\dfrac{2}{c}+\dfrac{3}{a}\left(2\right)\\\dfrac{36}{c+2a+3b}\le\dfrac{1}{c}+\dfrac{2}{a}+\dfrac{3}{b}\left(3\right)\end{matrix}\right.\)
Lấy (1) + (2) + (3) ta được:
\(36F\le6\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=6.3=18\)
\(\Rightarrow F\le\dfrac{1}{2}\)
MaxF=1/2 khi \(a=b=c=1\)
Đúng 4
Bình luận (0)
tìm a để biểu thức có nghĩa:
a) \(\sqrt{\dfrac{-a}{3}}\)
b) \(-\sqrt{\dfrac{1}{a^2}}\)
c) \(\sqrt{\dfrac{\left(1-a\right)^3}{a^2}}\)
d) \(\sqrt{\dfrac{a^{2^{ }}+1}{1-2a}}\)
e) \(\sqrt{a^2-1}\)
f) \(\sqrt{\dfrac{2a-1}{2-a}}\)
a) Để biểu thức có nghĩa thì \(\dfrac{-a}{3}\ge0\Rightarrow a\le0\)
b) Để biểu thức có nghĩa thì \(\dfrac{1}{a^2}\ge0\) (luôn đúng)
c) Để biểu thức có nghĩa thì \(\dfrac{\left(1-a\right)^3}{a^2}\ge0\Rightarrow\left\{{}\begin{matrix}\left(1-a\right)^3\ge0\\a\ne0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}1-a\ge0\\a\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}a\le1\\a\ne0\end{matrix}\right.\)
d) Để biểu thức có nghĩa thì \(\dfrac{a^2+1}{1-2a}\ge0\Rightarrow1-2a>0\Rightarrow a< \dfrac{1}{2}\)
e) Để biểu thức có nghĩa thì \(a^2-1\ge0\Rightarrow a^2\ge1\Rightarrow\left|a\right|\ge1\)
f) Để biểu thức có nghĩa thì \(\Rightarrow\dfrac{2a-1}{2-a}\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2a-1\ge0\\2-a>0\end{matrix}\right.\\\left\{{}\begin{matrix}2a-1\le0\\2-a< 0\end{matrix}\right.\end{matrix}\right.\)
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a\ge\dfrac{1}{2}\\a< 2\end{matrix}\right.\\\left\{{}\begin{matrix}a\le\dfrac{1}{2}\\a>2\end{matrix}\right.\left(l\right)\end{matrix}\right.\Rightarrow\dfrac{1}{2}\le a< 2\)
Đúng 2
Bình luận (0)
BT1: a) 2x-10 ; b) 3x-25+x ; c) 2(x-3)-43(1+x)-5x ; d) dfrac{x+1}{2}- dfrac{2x}{3}1 ; e) x(x-2)+3(x-2)0 ; f) dfrac{x+1}{x-1}+ dfrac{3}{x} dfrac{x^2+2}{x^2-x}BT2: a) Cho ab, chứng minh rằng 2a+12b-3b) Tìm x để giá trị của biểu thức 3x-1 ≤ giá trị biểu thức x+2c) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số (mng giúp mình giải phương trình thôi nha)2x+30 ; 3x+1x-4 ; 2(x+1)+3≥ 3(5-x) ; dfrac{x}{3}-dfrac{x+1}{5}1BT3: Giải bài toán bằng cách lập phương trình 1 ô tô đi từ A đế...
Đọc tiếp
BT1:
a) 2x-1=0 ; b) 3x-2=5+x ; c) 2(x-3)-4=3(1+x)-5x ; d) \(\dfrac{x+1}{2}\)- \(\dfrac{2x}{3}\)=1 ; e) x(x-2)+3(x-2)=0 ; f) \(\dfrac{x+1}{x-1}\)+ \(\dfrac{3}{x}\)= \(\dfrac{x^2+2}{x^2-x}\)
BT2:
a) Cho a>b, chứng minh rằng 2a+1>2b-3
b) Tìm x để giá trị của biểu thức 3x-1 ≤ giá trị biểu thức x+2
c) Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số (mng giúp mình giải phương trình thôi nha)
2x+3>0 ; 3x+1<x-4 ; 2(x+1)+3≥ 3(5-x) ; \(\dfrac{x}{3}\)-\(\dfrac{x+1}{5}\)>1
BT3: Giải bài toán bằng cách lập phương trình
1 ô tô đi từ A đến B với vận tốc 50km/h. Đến B, ô tô nghỉ lại 1h, sau đó quay trở về A với vận tốc 60km/h. Tổng thời gian đi và về(gồm thời gian nghỉ lại) là 6h30p. Tính quãng đường AB?
Mng giúp mình với mai mình kiểm tra rồi ạ, mình cảm ơn
2 tháng 5 2021 lúc 22:33
Cho biểu thức:
\(F=\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-1}-\dfrac{\sqrt{a}-1}{\sqrt{a}+1}+4\sqrt{a}\right)\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\)
a) Rút gọn F
b) Tìm a để F nhỏ nhất
c) Tìm a để \(\sqrt{F}>F\)
d) So sánh F với \(\dfrac{1}{\sqrt{a}}\)
Tìm a để các hàm số
f
(
x
)
4
x
+
1
-
1
a
x
2
+
(...
Đọc tiếp
Tìm a để các hàm số f ( x ) = 4 x + 1 - 1 a x 2 + ( 2 a + 1 ) x k h i x ≠ 0 3 k h i x = 0 liên tục tại x = 0.
A. 1 2
B. 1 4
C. - 1 6
D. 1
- Ta có:
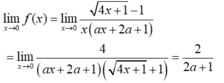
→ Hàm số không liên tục tại x = 0.
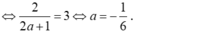
Chọn C.
Đúng 0
Bình luận (0)
2. Một hàm số được cho bằng bảng sau : X-2-1-dfrac{1}{2}0dfrac{1}{2}122Y1dfrac{1}{2}dfrac{1}{4}0-dfrac{1}{4}-dfrac{1}{2}-1-1dfrac{1}{2}a) Tìm f( 1); − f(1) ; f(2).b) Hàm số này có thể được cho bằng công thức nào ?
Đọc tiếp
2. Một hàm số được cho bằng bảng sau :
| X | -2 | -1 | \(-\dfrac{1}{2}\) | 0 | \(\dfrac{1}{2}\) | 1 | 2 | 2 |
| Y | 1 | \(\dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 0 | \(-\dfrac{1}{4}\) | \(-\dfrac{1}{2}\) | -1 | \(-1\dfrac{1}{2}\) |
a) Tìm f( 1); − f(1) ; f(2).
b) Hàm số này có thể được cho bằng công thức nào ?
a) Cho hàm số f(x) sao cho với mọi x khác 0 ta có f(x) f(dfrac{1}{x})+f(1)6.Tính f(-1)
b) Tìm số nguyên x sao cho: (x2x2 -1)(x2x2-4)(x2x2-7)(x2x2-10)0
Đọc tiếp
a) Cho hàm số f(x) sao cho với mọi x khác 0 ta có f(x) =f(\(\dfrac{1}{x}\))+f(1)=6.Tính f(-1)
b) Tìm số nguyên x sao cho: (x -1)(-4)(-7)(-10)<0
Cho hàm số f(x)=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tìm các g/trị của x để hàm số xác định
b) Tính f(\(4-2\sqrt{3}\)) và f(\(a^2\)) với a< -1
c) Tìm x sao cho f(x)=f(\(x^2\))