a) Xét ΔOAB và ΔOCD có 

\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\left(=\dfrac{3}{2}\right)\)

\(\widehat{AOB}\) chung

Do đó: ΔOAB\(\sim\)ΔOCD(c-g-c)

a) Do G là trọng tâm tam giác ABC nên AG = 2GM. Lại có AG = GD nên GD = 2GM hay GM = DM.

Xét tam giác DMB và tam giác GMC có:

DM = GM

BM = CM

\(\widehat{DMB}=\widehat{GMC}\)   (Hai góc đối đỉnh)

\(\Rightarrow\Delta DMB=\Delta GMC\left(c-g-c\right)\)

\(\Rightarrow BD=CG\)

b) Do \(\Delta DMB=\Delta GMC\Rightarrow\widehat{FBM}=\widehat{ECM}\)

Xét tam giác FBM và tam giác ECM có:

\(\widehat{FMB}=\widehat{EMC}=90^o\)

BM = CM

\(\widehat{FBM}=\widehat{ECM}\)

\(\Rightarrow\Delta FBM=\Delta ECM\)   (Cạnh góc vuông - góc nhọn kề)

\(\Rightarrow BF=CE\left(đpcm\right)\)

Gọi E là trung điểm KL; I là trung điểm AG

\(\left\{{}\begin{matrix}KE=EL\\BD=DC\end{matrix}\right.\Rightarrow ED\) là đtb hthang \(BCLK\left(BK//LC.do.cùng.\perp KL\right)\)

\(\Rightarrow ED=\dfrac{BK+CL}{2}\Rightarrow2ED=BK+CL\left(1\right)\)

Vì G là trọng tâm tam giác ABC nên \(GD=\dfrac{1}{2}AG\)

Mà \(AI=IG=\dfrac{1}{2}AG\) nên \(GD=AI=IG\)

Ta có \(ED//BK//LC\left(t/c.đtb\right)\Rightarrow ED\perp KL\left(BK\perp KL\right)\)

Áp dụng định lí Ta-lét cho \(AH//ED\left(\perp KL\right)\) ta có

\(\dfrac{AH}{ED}=\dfrac{AG}{GD}=2\Rightarrow AH=2ED\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow AH=BK+CL\)

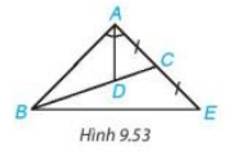
C là trung điểm của AE

\( \Rightarrow \) BC là trung tuyến của tam giác ABE (1)

D thuộc BC, \(BD = 2DC \Rightarrow BD = 2\left( {BC - BD} \right) \Rightarrow 3BD = 2BC \Rightarrow BD = \dfrac{2}{3}BC\)(2)

Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE

\( \Rightarrow \) AD là đường trung tuyến ứng với BE

Mà AD là đường phân giác của \(\widehat {BAC}\)

\( \Rightarrow \) Tam giác ABE cân tại A. 

Lấy P là trung điểm của BC;E là trung điểm của AG.Lần lượt lấy K,Q là hình chiếu của P và E xống đường thẳng d.

Do G là trọng tâm nên \(AG=\frac{2}{3}GP\Rightarrow EG=GP\)

Xét \(\Delta\)EKG và \(\Delta\)PQG có:\(EG=GP;\widehat{EGK}=\widehat{PGQ}\left(đ.đ\right);\widehat{EKG}=\widehat{PQG}\left(=90^0\right)\)

\(\Rightarrow\Delta EKG=\Delta PQG\left(ch-gn\right)\Rightarrow EK=PQ\)

Xét \(\Delta\)AMG có EK//AM;E là trung điểm của AG nên K là trung điểm của MG 

=> EK là đường trung bình => \(EK=\frac{1}{2}AM\)

Do EK=PQ nên \(PQ=\frac{1}{2}AM\)

Xét tứ giác BNFC có \(\widehat{N}=\widehat{F}=90^0\) nên nó là hình thang.

Mà hình thang BNFC có PQ là đường trung bình nên \(PQ=\frac{BN+FC}{2}\)

\(\Rightarrow\frac{AM}{2}=\frac{BN+FC}{2}\Rightarrow AM=BN+FC\left(đpcm\right)\)