a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow AC^2=35^2-21^2=784\)

hay AC=28cm

Xét ΔBAC vuông tại A có 

\(\sin\widehat{ABC}=\dfrac{AC}{BC}=\dfrac{4}{5}\)

nên \(\widehat{ABC}\simeq53^0\)

\(\Leftrightarrow\widehat{ACB}=37^0\)

BC=2*AM=10cm

AC=căn 10^2-6^2=8cm

AH=6*8/10=4,8cm

BH=AB^2/BC=6^2/10=3,6cm

MH=căn 5^2-4,8^2=1,4cm

Xét tam giác ABH vuông tại H, ta có:

\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)

\(\Rightarrow AB=5\left(cm\right)\)

Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:

\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)

Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)

AM là đường trung tuyến trong tam giác vuông ABC

=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)

a) Xét ΔABC có BD là đường phân giác ứng với cạnh AC(Gt)

nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)(Tính chất đường phân giác của tam giác)

\(\Leftrightarrow\dfrac{AB}{3}=\dfrac{BC}{5}\)

Ta có: AD+CD=AC(D nằm giữa A và C)

nên AC=3+5=8(cm)

Đặt \(\dfrac{AB}{3}=\dfrac{BC}{5}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}AB=3k\\BC=5k\end{matrix}\right.\)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\left(3k\right)^2+8^2=\left(5k\right)^2\)

\(\Leftrightarrow9k^2+64=25k^2\)

\(\Leftrightarrow16k^2=64\)

\(\Leftrightarrow k^2=4\)

hay k=2

Suy ra: \(\left\{{}\begin{matrix}AB=3\cdot k=3\cdot2=6\left(cm\right)\\BC=5\cdot k=5\cdot2=10\left(cm\right)\end{matrix}\right.\)

Vậy: AB=6cm; BC=10cm

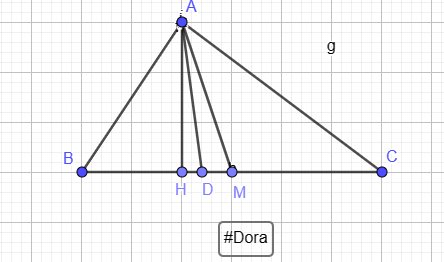
Vì `\triangle ABC` vuông tại `A` có `AM` là đường trung tuyến

    `=>AM=MC=1/2BC =>BC =40(cm)`

`@` Xét `\triangle ABC` vuông tại `A` có: `AC=\sqrt{BC^2 -AB^2}=32(cm)` (Py-ta-go)

`@` Mặt khác: Ta có `AH` là đường cao

    `=>BH=[AB^2]/[BC]` (Ht giữa cạnh và đường cao)

   `=>BH =14,4(cm)`

`@` Ta có: `HM =BC-BH-MC=5,6(cm)`

\(HC=\dfrac{3^2}{4}=2.25\left(cm\right)\)

BC=HB+HC=6,25(cm)

AM=BC/2=3,125(cm)

\(AB=\sqrt{4\cdot6.25}=5\left(cm\right)\)

\(AC=\sqrt{6.25^2-5^2}=3.75\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABH\) vuông tại \(H\) , ta có :

\(AB^2=AH^2+HB^2=3^2+4^2=25\Rightarrow AB=5\left(cm\right)\)

+ ) áp dụng hệ thức về cạnh và đường cao trong tam giác vuông \(ABC\) với \(AH\) là đường cao , ta có :

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{AH^2}-\dfrac{1}{AB^2}\) 

\(\Leftrightarrow\) \(\dfrac{1}{AC^2}=\dfrac{1}{3^2}-\dfrac{1}{5^2}=\dfrac{16}{225}\) 

\(\Rightarrow AC=\dfrac{15}{4}\left(cm\right)\)

+ ) áp dụng định lí Pytago trong tam giác vuông \(ABC\) vuông tại \(A\) , ta có :

\(BC^2=AB^2+AC^2=5^2+\left(\dfrac{15}{4}\right)^2=\dfrac{625}{16}\)

\(\Rightarrow BC=\dfrac{25}{4}\left(cm\right)\)

+ ) tam giác \(ABC\) vuông tại \(A\) có trung tuyến \(AM\) nên ta có :

\(AM=\dfrac{1}{2}BC=\dfrac{25}{8}\left(cm\right)\)

giupspp toi zưiiii