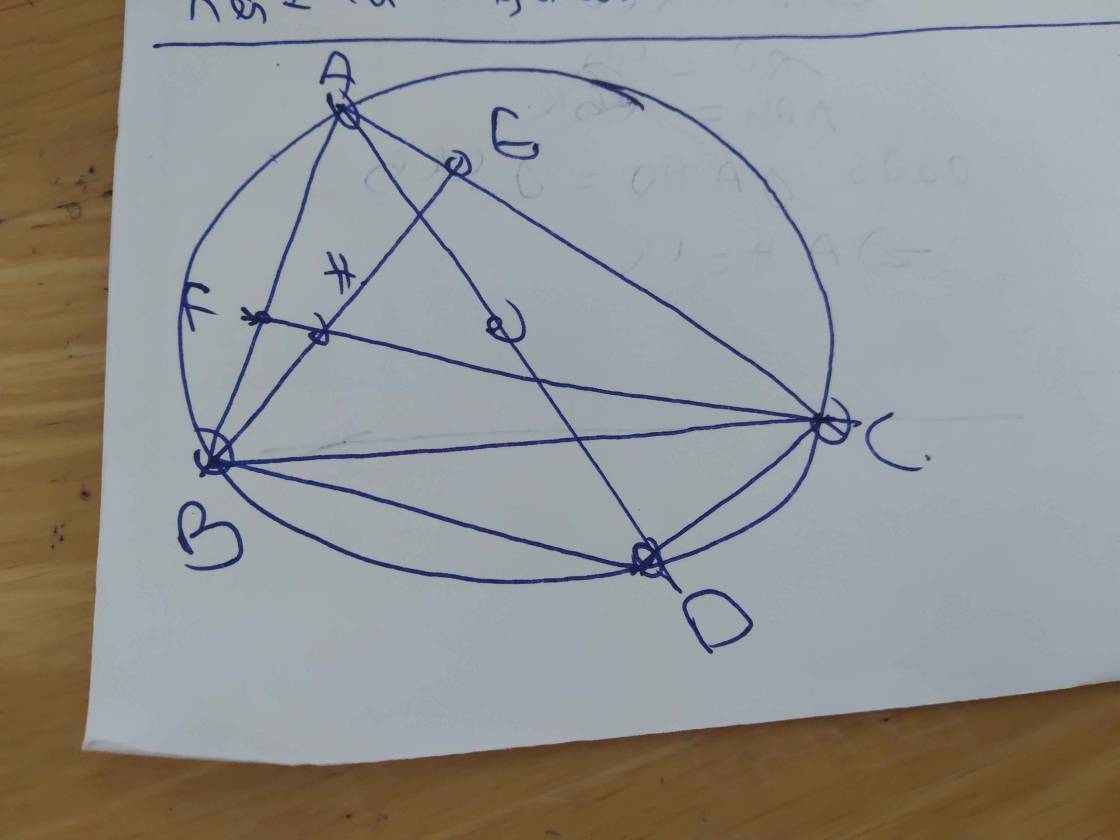
Cho tam giác ABC nội tiếp đường tròn tâm O.2 đường cao BE, CF cắt nhau tại H; AO cắt (O) tại S. các đường thẳng qua E, F song song với AS cắt BC tại M, N. Chứng minh rằng BM = CN

Những câu hỏi liên quan
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF 2
Đọc tiếp
Câu 5 (3,0 điểm). Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O. Các đường cao
AD, BE, CF của tam giác ABC cắt nhau tại H.
a) Chứng minh các tứ giác AEHF, BFEC nội tiếp đường tròn.
b) Đường thẳng AO cắt đường tròn tâm O tại điểm K khác điểm A. Gọi I là giao điểm của
hai đường thẳng HK và BC. Chứng minh I là trung điểm của đoạn thẳng BC.
c, tinh AH/AD + BH/BE + CH/CF =2
rightarrow Gấp Ạ! Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H a) Chứng minh : tứ giác AEHF, BFEC nội tiếp đường tròn b) Đường thẳng AO cắt đưởng tròn tâm O tại K khác điểm A . Gọi I là giao điểm của 2 đường thẳng HK và BC . Chứng minh I là trung điểm của đoạn BC c) Tính : AH/AD + BH/BE + CH/CF ( bỎ QUA phần này cũng đc ạ )
Đọc tiếp
\(\rightarrow\) Gấp Ạ!
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh : tứ giác AEHF, BFEC nội tiếp đường tròn
b) Đường thẳng AO cắt đưởng tròn tâm O tại K khác điểm A . Gọi I là giao điểm của 2 đường thẳng HK và BC . Chứng minh I là trung điểm của đoạn BC
c) Tính : AH/AD + BH/BE + CH/CF ( bỎ QUA phần này cũng đc ạ )
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H và lần lượt cắt đường tròn tại M, N, P. Chứng minh rằng:
1) Tứ giác BFEC và AEDB nội tiếp.
2) AE.AC = AF.AB.
3) Chứng minh H là tâm đường tròn nội tiếp tam giác EFD.
1: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BFEC là tứ giác nội tiếp
Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó: AEDB là tứ giác nội tiếp
2: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAFC
Suy ra: AE/AF=AB/AC
hay \(AE\cdot AC=AB\cdot AF\)
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB = AC) nội tiếp đường tròn tâm (O) các đường cao AG, BE, CF cắt nhau tại H. Chứng minh rằng tứ giác AEHF nội tiếp
góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
Đúng 0
Bình luận (0)
cho tam giác ABC nội tiếp trong đường tròn tâm O , BE và CF là hai đường cao , cắt nhau tại H , tứ giác AFHE nội tiếp trong đường tròn tâm I , BECF nội tiếp đường trfonf tâm M , chứng minh ME là tiếp tuyến của đương tròn tâm I
Xét tứ giác AFHE có
\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)
=>AFHE là tứ giác nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
=>IA=IH=IE=IF
Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp đường tròn đường kính BC
=>M là trung điểm của BC
=>MB=MC=ME=MF
Gọi O là giao điểm của AH với BC
Xét ΔABC có
BE,CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại O
ΔBHO vuông tại O
=>\(\widehat{OHB}+\widehat{OBH}=90^0\)
mà \(\widehat{OBH}+\widehat{OCE}=90^0\)(ΔBEC vuông tại E)
nên \(\widehat{OHB}=\widehat{OCE}\)
mà \(\widehat{OHB}=\widehat{IHE}\)(hai góc đối đỉnh)
nên \(\widehat{IHE}=\widehat{OCE}\)
IH=IE
=>\(\widehat{IHE}=\widehat{IEH}\)
mà \(\widehat{IHE}=\widehat{OCE}\)
nên \(\widehat{IEH}=\widehat{OCE}=\widehat{ECB}\)
ME=MB
=>ΔMEB cân tại M
=>\(\widehat{MEB}=\widehat{MBE}\)
=>\(\widehat{MEB}=\widehat{EBC}\)
\(\widehat{IEM}=\widehat{IEH}+\widehat{MEH}\)
\(=\widehat{EBC}+\widehat{ECB}\)
\(=90^0\)
=>ME là tiếp tuyến của (I)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF cắt nhau tại H. Vẽ tiếp tuyến của đường tròn O tại A. Đường thẳng EF cắt đường tròn O tại I Và K a) CM: các tứ giác BFHD,BFEC nội tiếp b) CM:EB là tia phân giác của góc FED c)CM: OA vuông góc IK d) gọi S là tâm đường tròn ngoại tiếp tam giác BCE,đường thẳng vuô g góc với HS tại S cắt AB tại P, cắt AC tạ...
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF cắt nhau tại H. Vẽ tiếp tuyến của đường tròn O tại A. Đường thẳng EF cắt đường tròn O tại I Và K a) CM: các tứ giác BFHD,BFEC nội tiếp b) CM:EB là tia phân giác của góc FED c)CM: OA vuông góc IK d) gọi S là tâm đường tròn ngoại tiếp tam giác BCE,đường thẳng vuô g góc với HS tại S cắt AB tại P, cắt AC tại Q và cắt AD tại G. Chứng minh PG=GQ
a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK
Đúng 1
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O. Hai đường cao BE và CF cắt nhau tại H. Tia AO cắt đường tròn tại D . Chứng minh
a) tứ giác AEHF nội tiếp đường tròn
B) tứ giác BHCD là hình bình hành
c) tứ giác BFEc nội tiếp được đường tròn
d) Tam giác AEF ~ tam giác ABC, suy ra AE.AC = AF.AB
a) Xét tứ giác AEHF có
\(\widehat{HFA}\) và \(\widehat{HEA}\) là hai góc đối
\(\widehat{HFA}+\widehat{HEA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: AEHF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. Cho tam giác abc nhọn nội tiếp đường tròn tâm O. Hai đường cao BE, CF của tam giác ABC cắt nhau tại H
a) Chứng minh tứ giác BFEC nội tiếp đường tròn
b) Chứng minh rằng AF.AB=AE.AC
c) Kẻ đường kính AD của đường tròn tâm O. Chứng minh tứ giác BHCD là hình bình hành
Cho tam giác ABC nhọn nội tiếp đường tròn (O), 2 đường cao BE và CF của tam giác ABC cắt nhau tại H. Chứng minh: a. Tứ giác BCEF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác BCEF. b. CM: AE.AC = AF.AB c. Tia AO cắt đường tròn (O) tại P, cắt EF tại Q. CM AP vuông góc với EF
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại Ha) Chứng minh : tứ giác AEHF, BFEC nội tiếp đường trònb) Đường thẳng AO cắt đưởng tròn tâm O tại K khác điểm A . Gọi I là giao điểm của 2 đường thẳng HK và BC . Chứng minh I là trung điểm của đoạn BC c) Tính : AH/AD + BH/BE + CH/CF
Đọc tiếp
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh : tứ giác AEHF, BFEC nội tiếp đường tròn
b) Đường thẳng AO cắt đưởng tròn tâm O tại K khác điểm A . Gọi I là giao điểm của 2 đường thẳng HK và BC . Chứng minh I là trung điểm của đoạn BC
c) Tính : AH/AD + BH/BE + CH/CF
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC
Đúng 0
Bình luận (0)