Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
AOC ^ = AIC ^
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
A O C ^ = A I C ^
Cho đường tròn (O) và hai day cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD) ; AD cắt BC tại I. Chứng minh \(\widehat{AOC}=\widehat{AIC}.\)
Theo giả thiết: cung AC = cung BD (vì AB // CD) (1)
\(\widehat{AIC}\) = sđ cung AC + cung BD : 2 (2)
Theo (1) suy ra \(\widehat{AIC}\) = sđ cung AC
\(\widehat{AOC}\) = sđ cung AC(góc ở tâm chắn cung AC)
So sánh (3), (4), ta có \(\widehat{AOC}\) = \(\widehat{AIC}\)
Cho đường tròn (O) đường kính AB = 2R và dây cung CD = R (C, D nằm trên cùng nửa mặt phẳng có bờ AB, điểm C nằm trên cung AD). Gọi P là giao điểm của AC và BD, Q là giao điểm của AD và BC, Q là giao. Tính số đo góc APB và AQB.
Do \(OC=OD=CD=R\Rightarrow\Delta OCD\) là tam giác đều
\(\Rightarrow\widehat{COD}=60^0\)
Mà \(\widehat{CAD}=\dfrac{1}{2}\widehat{COD}\) (góc nt và góc ở tâm cùng chắn CD)
\(\Rightarrow\widehat{CAD}=30^0\)
AB là đường kính nên \(\widehat{ADB}\) là góc nt chắn nửa đường tròn \(\Rightarrow\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{ADP}=90^0\Rightarrow\widehat{APB}=180^0-\left(90^0+30^0\right)=60^0\)
Tương tự ta có \(\widehat{ACB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=90^0\Rightarrow\widehat{BCP}=90^0\)
\(\Rightarrow\widehat{CQD}=360^0-\left(\widehat{APB}+\widehat{ADP}+\widehat{ACB}\right)=360^0-\left(60^0+90^0+90^0\right)=120^0\)
\(\Rightarrow\widehat{AQB}=\widehat{CQD}=120^0\) (2 góc đối đỉnh)
Cho hai đoạn thẳng AB và CD song song và bằng nhau, sao cho A và C nằm trên hai nửa mặt phẳng đối nhau có bờ chứa BD. Gọi O là giao của AC và BD. Chứng minh O là trung điểm của AC và BD.
BÀI NÀY KHÓ QUÁ ! CÁC THÁNH TOÁN ƠI GIÚP VỚI :(
Cho đường tròn (O;R) đường kính AB. Gọi M,N lần lượt là trung điểm của OA và OB. QUA M,N lần lượt vẽ các dây CD và EF song song với nhau ( C và E nằm cùng một nửa mặt phẳng có bờ AB )
a) CM : CDEF là hình chữ nhật.
b) giả sử CD và EF cùng tạo với AB một góc 30°. tính diện tích CDFE.
a) qua O kẻ OPQ vuông góc với CD ; EF ( P thuộc CD; Q thuộc EF)
=> P C =PD ; QE =QF (1)
+ Mặt khác tam giác POM = QON ( cạnh huyền - góc nhọn)
=>OP =OQ
=> CD = EF (2)
(1)(2) => PC = QE mà PC//QE , P=Q =90 => PQCE là HCN
tương tự => PQFD là HCN
=> CDEF có 4 góc vuông là HCN
b)Xét tm giác POM vuông tại P có M =30
sin M = OP/OM => OP =OM.sin30 = R/2 . 1/2 = R/4
=> PQ = R/2 (3)
+ Tam giác POC uông tạ P => CP =\(\sqrt{R^2-\left(\frac{R}{4}\right)^2}=\frac{R\sqrt{15}}{4}\Rightarrow CD=\frac{R\sqrt{15}}{2}\)(4)
Từ (3)(4) => S =
Cho nửa đường tròn tâm O có đường kính AB . Gọi Ax , By là hai tiếp tuyến vẽ từ A đến B ( Ax , By và nửa đường tròn cùng thuộc nửa mặt phẳng bờ AB) . Qua điểm thuộc nửa đường tròn ( M khác A và B ) kẻ tiếp tuyến thứ ba , tiếp tuyến này cắt Ax và By lần lượt tại điểm C và D 1. Chứng minh CD=AC+BD.
2. Gọi N là giao điểm của AD và BC chứng minh MN song song với AC.
a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC
Cho ba đường thẳng cắt nhau tại ba giao điểm A, B, C.
a. Hãy vẽ điểm O sao cho A và O nằm trong một nửa mặt phẳng có bờ là BC, B và O nằm trong một nửa mặt phẳng có bờ là đường thẳng CA và C và O nằm trong một nửa mặt phẳng có bờ là đường thẳng AB.
b. Hãy vẽ điểm A’ sao cho A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AB đồng thời A’ và O nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng AC. A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng nào?
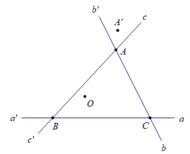
a. Giả sử ba đường thẳng aa’, bb’ và cc’ cắt nhau từng đôi một tại ba điểm A, B, C (hình vẽ). Điểm O cần vẽ là giao điểm của hai tia AO và BO sao cho tia AO nằm giữa hai tia AB và AC, tia BO nằm giữa hai tia BA và BC.
b. Điểm A’ nằm trên tia AA’ sao cho tia AA’ nằm giữa hai tia Ab’ và Ac, A’ và O cùng nằm trong một nửa mặt phẳng có bờ là đường thẳng BC.
: Cho đường tròn tâm ( O; 5cm ), hai dây AB, CD song song với nhau, có độ dài lần lượt là 8cm và 9,6cm. Tính khoảng cách giữa hai dây đó, biết tâm O nằm trong phần mặt phẳng giới hạn bới hai dây AB và CD.
Từ O kẻ đường thẳng vuông góc AB và CD, cắt AB và CD lần lượt tại H và K
\(\Rightarrow\) H là trung điểm AB và K là trung điểm CD
\(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=4\\CK=\dfrac{1}{2}CD=4,8\end{matrix}\right.\)
Áp dụng định lý Pitago cho tam giác vuông OAH (với chú ý \(OA=OC=R=5\))
\(OH=\sqrt{OA^2-AH^2}=3\left(cm\right)\)
Pitago tam giác OCK:
\(OK=\sqrt{OC^2-CK^2}=1,4\left(cm\right)\)
\(\Rightarrow HK=OH+OK=4,4\left(cm\right)\)
Cho nửa đường tròn tâm O, đường kính AB. Kẻ tia Ax vuông góc với AB ( tia Ax và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB. Lấy một điểm C bất kì thuộc nửa đường tròn ( C khác A và B). Qua O kẻ một đường thẳng song song với BC cắt tia Ax tại M và cắt AC tại F. a, Tính MB biết BC = 5 , AC = 8 b, D là giao MB và (O) cmr ∆MFD ~ ∆MBO