Các câu hỏi tương tự
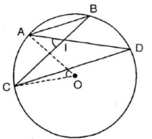
Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:
A O C ^ = A I C ^
Cho đường tròn tâm O đường kính AB. Từ A và B vẽ hai dây cung AC và BD của đường tròn (O) cắt nhau tại N bên trong đường tròn (C,D nằm trên cùng nửa mặt phẳng bờ AB). Hai tiếp tuyến Cx, Dy của đường tròn (O) cắt nhau tại M. Gọi P là giao điểm của hai đường thẳng AD và BC
1. Chứng minh tứ giác DNCP nội tiếp đường tròn
2. Chứng minh ba điểm P, M, N thẳng hàng
Cho nửa đường tròn (O) đường kính AB 2R. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. M là điểm trên (O) sao cho tiếp tuyên tại M cắt Ax, By tại D và C. Đường thẳng AD cắt BC tại Na, Chứng minh A, C, M, O cùng thuộc một đường tròn. Chỉ ra bán kính của đường tròn đób, Chứng minh OC và BM song songc, Tìm vị trí điểm M sao cho SACDB nhỏ nhấtd, Chứng minh MN và AB vuông góc nhau
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB = 2R. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. M là điểm trên (O) sao cho tiếp tuyên tại M cắt Ax, By tại D và C. Đường thẳng AD cắt BC tại N
a, Chứng minh A, C, M, O cùng thuộc một đường tròn. Chỉ ra bán kính của đường tròn đó
b, Chứng minh OC và BM song song
c, Tìm vị trí điểm M sao cho SACDB nhỏ nhất
d, Chứng minh MN và AB vuông góc nhau
Cho nửa đường tròn tâm O có đường kính AB . Gọi Ax , By là hai tiếp tuyến vẽ từ A đến B ( Ax , By và nửa đường tròn cùng thuộc nửa mặt phẳng bờ AB) . Qua điểm thuộc nửa đường tròn ( M khác A và B ) kẻ tiếp tuyến thứ ba , tiếp tuyến này cắt Ax và By lần lượt tại điểm C và D 1. Chứng minh CD=AC+BD.
2. Gọi N là giao điểm của AD và BC chứng minh MN song song với AC.
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F a) chứng minh BDCF là tứ giác nội tiếp đường trònb) chứng minh CD2 CE.CFc) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB d) K...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F
a) chứng minh BDCF là tứ giác nội tiếp đường tròn
b) chứng minh CD2 =CE.CF
c) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB
d) Khi EF là tiếp tuyến của nửa đường tròn đường kính AB thì D nằm ở vị trí nào trên AB
Cho nửa đường tròn (O) đường kính AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. Điểm M nằm trên (O) sao cho tiếp tuyến tại M cắt Ax, By tại D và C. Chứng minh:a, AD + BC CDb,
C
O
D
^
90
0
c, AC.BD
O
A...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Trên cùng nửa mặt phẳng bờ AB vẽ hai tiếp tuyến Ax, By. Điểm M nằm trên (O) sao cho tiếp tuyến tại M cắt Ax, By tại D và C. Chứng minh:
a, AD + BC = CD
b, C O D ^ = 90 0
c, AC.BD = O A 2
d, AB là tiếp tuyến của đường tròn đường kính CD
Cho hai đường tròn (O;R) và (O;R) cắt nhau tại A và B. (O và O nằm ở hai nửa mặt phẳng bờ AB.) Một đường thẳng qua A cắt đường tròn (O) và (O) tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE song song với KD (E thuộc BD).a/ Chứng minh tam giác BOO đồng dạng với tam giác BCD.b/ Chứng minh tứ giác BCKD là tứ giác nội tiếpc/ Chứng minh AE là tiếp tuyến của đường tròn (O;R)d/ Tìm vị trí của CD để diện tích tam giác BCD...
Đọc tiếp
Cho hai đường tròn (O;R) và (O';R') cắt nhau tại A và B. (O và O' nằm ở hai nửa mặt phẳng bờ AB.) Một đường thẳng qua A cắt đường tròn (O) và (O') tương ứng tại C và D (A nằm giữa C và D). Các tiếp tuyến tại C và D của hai đường tròn cắt nhau tại K. Nối KB cắt CD tại I. Kẻ IE song song với KD (E thuộc BD).
a/ Chứng minh tam giác BOO' đồng dạng với tam giác BCD.
b/ Chứng minh tứ giác BCKD là tứ giác nội tiếp
c/ Chứng minh AE là tiếp tuyến của đường tròn (O;R)
d/ Tìm vị trí của CD để diện tích tam giác BCD lớn nhất
từ điểm A nằm ngoài đường tròn (O). kẻ hai tiếp tuyến AB và AC( B,C là hai tiếp điểm). kẻ dây cung BD song song AC( tia AD nằm giữa hai dây AB và AO). đường thẳng AD cắt đường tròn O tại E và BC tại I. Tia BE cắt AC tại K.a) CMinh: AB^2AD. AEb) chứng minh : K là trung điểm của ACc) kẻ đường kính CS của đường tròn (O) và SE cắt BC ở M. chứng minh: MB.CI MI.CBcả nhà giải giúp e câu B và câu C với a. tks mọi người
Đọc tiếp
từ điểm A nằm ngoài đường tròn (O). kẻ hai tiếp tuyến AB và AC( B,C là hai tiếp điểm). kẻ dây cung BD song song AC( tia AD nằm giữa hai dây AB và AO). đường thẳng AD cắt đường tròn O tại E và BC tại I. Tia BE cắt AC tại K.
a) CMinh: AB^2=AD. AE
b) chứng minh : K là trung điểm của AC
c) kẻ đường kính CS của đường tròn (O) và SE cắt BC ở M. chứng minh: MB.CI= MI.CB
cả nhà giải giúp e câu B và câu C với a. tks mọi người
Cho đường tròn O và hai dây AB, CD bằng nhau và các đường thẳng AB và CD cắt nhau tại điểm E. Biết rằng các điểm B và D nằm trong cùng nửa mặt phẳng bờ AC. Chứng minh:
a) EA=EC và AD=BC.
b) OE vuông góc với AC và DB.
Help me!!!! Thanks mn.