CHO TAM GIÁC ABC TRÊN TIA ĐỐI TIA BC LẤY BD=BA.TRÊN TIA ĐỐI TIA CB LẤY CA=CE .VẼ BH VUÔNG GÓC AD VÀ CK VUÔNG GÓC AE .CHỨNG MINH;
A> HK//DE
B> HK CẮT AB TẠI M VÀ CẮT AC TẠI N . CHỨNG MINH MN//BC VÀ MN=BC/2
C>TÍNH HK BIẾT CHU VI TAM GIÁC ABC=18CM
Những câu hỏi liên quan
Tam giác ABC, trên tia đối của tia BC lấy điểm D sao cho BD=BA.Trên tia đối của tia CB lấy điểm E sao cho CE=CA .Kẻ BH vuông góc AD,CK vuông góc AE.
CM: a) AH=HD
b) HK=BC
Bài 1: Tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD CE. Kẻ BH vuông góc với AD. Kẻ CK vuông góc với AE. Chứng minh rằng :a) Chứng minh: DADE cân và BH CK b) ABH ACKc) Gọi O là giao điểm của HB và KC. Chứng minh OBC cân.d) Chứng minh AO là tia phân giác của góc DAE e) Gọi I là trung điểm của BC. Chứng minh: A, I, O thẳng hàng.
Đọc tiếp
Bài 1: Tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD. Kẻ CK vuông góc với AE. Chứng minh rằng :
a) Chứng minh: DADE cân và BH = CK
b) ABH = ACK
c) Gọi O là giao điểm của HB và KC. Chứng minh OBC cân.
d) Chứng minh AO là tia phân giác của góc DAE
e) Gọi I là trung điểm của BC. Chứng minh: A, I, O thẳng hàng.
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó; ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
b: Ta có: ΔABH=ΔACK
nên \(\widehat{ABH}=\widehat{ACK}\)
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
Đúng 1
Bình luận (1)
c1
cho tam giác abc cân tại a trên tia đối tia bc lấy d và trên tia đối tia cb lấy e sao cho bd=ce vẽ bh vuông góc ad và ck vuông góc ae chứng minh bc song song hk
câu này khó quá nên mình ko làm đc các bạn giúp mình nha!!
Đúng 0
Bình luận (0)
do \(\Delta ABC\)cân tại A và \(BD=CE\)\(\Rightarrow\Delta ADE\)cũng cân tại A \(\Rightarrow AD=AE\left(4\right);\widehat{ADE}=\widehat{AED}\left(1\right)\)Xét hai tam giác vuông \(\Delta DHB,\Delta EKC\)có \(BD=CE\left(2\right);\widehat{DHB}=\widehat{EKC}=90^0\left(3\right)\)tứ 1,2,3 ta có \(\Delta DHB=\Delta EKC\Rightarrow DH=EK\left(5\right)\)tỪ 4,5 CÓ TỈ SỐ \(\frac{AH}{AD}=\frac{AK}{AE}\Rightarrow HK\downarrow\uparrow BC\)(dpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tai BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông với AD, kẻ CK vuông góc với AE. Chứng minh rằng: BH = CK
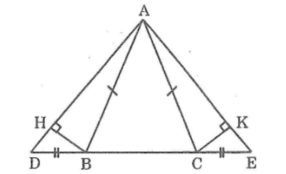
Vì ΔABC cân tại A nên∠(ABC) =∠(ACB) (tính chất tam giác cân)
Ta có: ∠(ABC) +∠(ABD) =180o(hai góc kề bù)
∠(ACB) +∠(ACE) =180o(hai góc kề bù)
Suy ra: ∠(ABD) =∠(ACE)
Xét ΔABD và ΔACE, ta có:
AB = AC (gt)
∠(ABD) =∠(ACE) (chứng minh trên)
BD=CE (gt)
Suy ra: ΔABD= ΔACE (c.g.c)
⇒∠D =∠E (hai góc tương ứng)
Xét hai tam giác vuông ΔBHD và ΔCKE, ta có:
∠(BHD) =∠(CKE) = 90º
BD=CE (gt)
∠D =∠E (chứng minh trên)
Suy ra: ΔBHD= ΔCKE (cạnh huyền – góc nhọn)
Suy ra: BH = CK (hai cạnh tương ứng)
Đúng 2
Bình luận (0)
Cho tam giác ABC , trên tia đối của tia BC lấy D sao cho BD= BA . Trên tia đối CB lấy E sao cho CE = CA . Kẻ BH vuông góc với AD, CK vuông góc với AE
a, AH=HD
b, HK // BC
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Kẻ BH vuông góc với AD, kẻ CK vuông góc với AE. Chứng minh rằng:
a, BH = CK
B, △ABH = △ACK
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và \(\widehat{D}=\widehat{E}\)
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do dó: ΔABH=ΔACK
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng : BD = CE
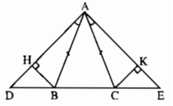
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..
Đúng 1
Bình luận (0)
Bài 3.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấyđiểm E sao cho BD = CE. Kẻ BH vuông góc với AD, kẻ CK vuông góc với AE. Chứng minh rằng:
a) BH = CK b) ∆ABH = ∆ACK
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó:ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\)
Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó:ΔABH=ΔACK
Đúng 3
Bình luận (0)
cho tam giác ABC cân tại A.Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD=CE. Kẻ BH vuông góc với AD , kẻ CK vuông góc với AE . Chứng minh rằng :
a) BH=CK
b)tam giác ABH=tam giác ACK
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
Đúng 1
Bình luận (0)