a) Thay x=-1 và y=4 vào (d), ta được:

\(3m\cdot\left(-1\right)+m-2=4\)

\(\Leftrightarrow-2m=6\)

hay m=-3

b) Để (d)//(Δ) thì \(\left\{{}\begin{matrix}3m=6\\m-2\ne-1\end{matrix}\right.\Leftrightarrow m=2\)

cho mình xin câu C với bạn !! :)

c)

`y=3mx+m-2`

`<=>3mx+m-2-y=0`

`<=>(3x+1)m-(y+2)=0`

`=> {(3x+1=0),(y+2=0):}`

`<=> {(x=-1/3),(y=-2):}`

Vậy điểm cố định mà d luôn đi qua là: `(-1/3 ; -2)`

a:

Sửa đề: \(I\left(\dfrac{1}{2};-3\right)\)

Thay \(x=\dfrac{1}{2};y=-3\) vào (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\), ta được:

\(\left(1-2m\right)\cdot\dfrac{1}{2}+m-\dfrac{7}{2}=-3\)

=>\(\dfrac{1}{2}-m+m-\dfrac{7}{2}=-3\)

=>\(\dfrac{1}{2}-\dfrac{7}{2}=-3\)

=>-3=-3(đúng)

vậy: I(1/2;-3) là điểm cố định mà (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\) luôn đi qua

b: \(\left(d\right):y=\left(2m+1\right)x+m-2\)

\(=2mx+x+m-2\)

\(=m\left(2x+1\right)+x-2\)

Điểm mà (d) luôn đi qua có tọa độ là:

\(\left\{{}\begin{matrix}2x+1=0\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{1}{2}-2=-\dfrac{5}{2}\end{matrix}\right.\)

\(a,d//d_1\Leftrightarrow\left\{{}\begin{matrix}m+2=-2\\m\ne3\end{matrix}\right.\Leftrightarrow m=-4\\ b,d\perp d_2\Leftrightarrow\dfrac{1}{3}\left(m+2\right)=-1\Leftrightarrow m+2=-3\Leftrightarrow m=-5\\ c,d.qua.N\left(1;3\right)\Leftrightarrow x=1;y=3\Leftrightarrow3=m+2+m\\ \Leftrightarrow2m=1\Leftrightarrow m=\dfrac{1}{2}\)

\(d,\) Gọi điểm đó là \(A\left(x_1;y_1\right)\)

\(\Leftrightarrow y_1=\left(m+2\right)x_1+m\\ \Leftrightarrow y_1-mx_1-2x_1-m=0\\ \Leftrightarrow-m\left(x_1+1\right)+y_1-2x_1=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_1+1=0\\y_1-2x_1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-1\\y_1=-2\end{matrix}\right.\)

Vậy \(A\left(-1;-2\right)\) luôn đi qua D với mọi m

a. d qua gốc tọa độ khi:

\(m-2=0\Rightarrow m=2\)

b. d cắt trục tung tại điểm có tung độ là 1/3 khi:

\(m-2=\dfrac{1}{3}\Rightarrow m=\dfrac{7}{3}\)

c. d qua A khi:

\(2\left(1-4m\right)+m-2=-3\)

\(\Rightarrow m=\dfrac{3}{7}\)

a, với d = -1

Ta có hàm số y = - \(x\) + 4 + 3 ⇒ y = -\(x\) + 7

+ Giao của đồ thị với trục o\(x\) là điểm có hoành độ thỏa mãn:

- \(x\) + 7 = 0 ⇒ \(x\) = 7 

Giao đồ thì với trục o\(x\) là A(7; 0)

+ Giao của đồ thị với trục oy là điểm có tung độ thỏa mãn:

y = 0 + 7 ⇒ y = 7

Giao đồ thị với trục oy là điểm B(7; 0)

Ta có đồ thị 

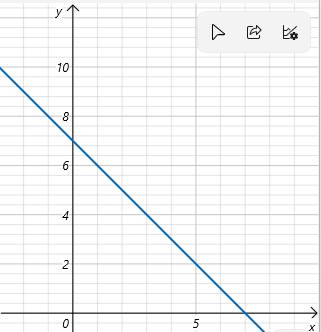
b, Đồ thị hàm số y = - m\(x\) + 4 - 3m (d)

(d) đi qua gốc tọa độ khi và chỉ tọa độ O(0; 0) thỏa mãn phương trình đường thẳng d

Thay tọa độ điểm O vào đường thẳng d ta có: 

      -m.0 + 4 - 3m = 0

                   4 - 3m = 0

                          m = \(\dfrac{4}{3}\)

c, để d cắt trục tung tại điểm - 4 khi và chỉ m thỏa mãn phương trình:

       -m.0 + 4 - 3m = - 4

                   4 - 3m = - 4

                         3m = 8

                            m = \(\dfrac{8}{3}\)

d, d cắt trục tung tại điểm - 2 khi và chỉ khi m thỏa mãn phương trình

        -m.0 + 4 - 3m = -2

                    4 - 3m = -2

                          3m = 6

                            m = 2

e, d song song với đường thẳng y = 2\(x\) + 3 khi và chỉ khi

    - m = 2 và 4 - 3m ≠ 3 ⇒ m ≠ \(\dfrac{1}{3}\)

       ⇒m = -2

f, d đi qua A (1;2) khi và chỉ m thỏa mãn phương trình:

     -m.(1) + 4 - 3m = 2

     -m - 3m = 2 - 4

       - 4m = -2 

          m =  \(\dfrac{1}{2}\)

a: Thay x=2 và y=1 vào (d), ta được:

2m-2+2=1

hay \(m=\dfrac{1}{2}\)

a) Để đường thẳng d: (2m-1)x+(m-2)y=m²-3 đi qua gốc tọa độ thì x=y=0

\(\Rightarrow m^2-3=0\Leftrightarrow\left(m-\sqrt{3}\right)\left(m+\sqrt{3}\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}m-\sqrt{3}=0\\m+\sqrt{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\sqrt{3}\\m=-\sqrt{3}\end{matrix}\right.\)

Vậy khi \(m=\left\{-\sqrt{3};\sqrt{3}\right\}\) thì d đi qua gốc tọa độ.

b) Để đường thẳng d: (2m-1)x+(m-2)y=m²-3 đi qua điểm A thì x=3, y=5.

\(\Rightarrow3\left(2m-1\right)+5\left(m-2\right)=m^2-3\)

\(\Leftrightarrow-m^2+11m-10=0\)

\(\Leftrightarrow m\left(1-m\right)-10\left(1-m\right)=0\)

\(\Leftrightarrow\left(1-m\right)\left(m-10\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}1-m=0\\m-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=10\end{matrix}\right.\)

Vậy khi \(m=\left\{1;10\right\}\) thì d đi qua gốc tọa độ.

Có một và chỉ một đường thẳng đi qua điểm M và song song với đường thẳng d