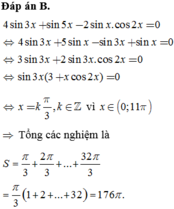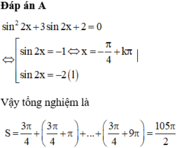1) tìm tất cả các nghiệm của phương trình:\(sin3x-\frac{2}{\sqrt{3}}sin^2x=2sinx.cos2x\) thuộc đoạn \(\left[0;2\pi\right]\)
2) tìm nghiệm của phương trình: \(sin^2x+sin^22x+sin^23x=\frac{3}{2}\) trong khoảng \(\left(\frac{-\pi}{2};\frac{\pi}{2}\right)\)
3) tìm nghiệm của phương trình: \(sin2x+sinx-\frac{1}{2sinx}-\frac{1}{2sinx}=2cot2x\) trong khoảng (0;\(\pi\))
4) phương trình cos22x+3cos18x+3cos14x+cos10x=0 có bao nhiêu nghiệm thuộc khoảng (0;\(\frac{\pi}{2}\))