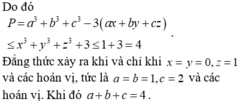a+b>= 2 căn ab

tương tự cộng theo vế với thu gọn

bạn có thể giải chi tiết hơn giúp mình dc k. Tks :v

\(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)

Theo AM-GM , ta có :

\(a+b\ge2\sqrt{ab}\)

\(b+c\ge2\sqrt{bc}\)

\(c+a\ge2\sqrt{ca}\)

Cộng vế theo vế , có :

\(2a+2b+2c\ge2\sqrt{ab}+2\sqrt{bc}+2\sqrt{ca}\)

\(\Rightarrow a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)

a) 

(a - 1) - (a - 3) = a - 1 - a + 3 = (-1) + 3 = 2

b) 

(2 + b) - (c + 1) = 2 + b - c - 1 = 1 + b - c 

a,=(-2)

vì a-a=0;1-3=(-2)

b,=(b-c)+1 

mik làm đúng thì k nhé

cảm mơn 2 pạn nhìu nha :D

Em tham khảo link:Câu hỏi của Conan Kudo - Toán lớp 8 - Học toán với OnlineMath

Ta có bổ đề

\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=0\)\(\Leftrightarrow\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}=\frac{3}{abc}\)

ÁP DỤNG BỔ ĐỀ VÀO P ta có

\(P=\frac{bc}{a^2}+\frac{ca}{b^2}+\frac{ab}{c^2}=abc\left(\frac{1}{a^3}+\frac{1}{b^3}+\frac{1}{c^3}\right)\)

\(=abc.\frac{3}{abc}=3\)

Vậy P=3

\(a\left(b-1\right)+b\left(1-c\right)+c\left(1-a\right)\le1\\ \Leftrightarrow-abc+ab+bc+ca-a-b-c+1\le2-abc\\ \Leftrightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)\le2-abc\)

lại có \(abc\le1\) nên \(2-abc\ge1\)

ta chứng minh \(\left(1-a\right)\left(1-b\right)\left(1-c\right)\le1\)

luôn đúng do \(0\le a;b;c\le1\)

vậy bđt dc cm

tick mik nhaaaaa.mik ms l9 thui

hi mik lớp 9

\(\left\{{}\begin{matrix}ab+bc+ca=abc\\a+b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}abc-ab-bc-ca=0\\a+b+c-1=0\end{matrix}\right.\)

\(\left(a-1\right)\left(b-1\right)\left(c-1\right)=\left(a-1\right)\left(bc-b-c+1\right)\)

\(=abc-ab-ac+a-bc+b+c-1\)

\(=\left(abc-ab-bc-ca\right)+\left(a+b+c-1\right)\)

\(=0+0=0\) (ddpcm)

\(VT=\left(a-1\right)\left(b-1\right)\left(c-1\right)\\ =\left(ab-a-b+1\right)\left(c-1\right)\\ =abc-ab-ac+a-bc+b+c-1\\ =abc-\left(ab+bc+ca\right)+\left(a+b+c\right)-1\\ =abc-abc+1-1=0=VP\)

Đáp án đúng : C

Không mất tính tổng quát, giả sử \(a\ge b\ge c\).

Khi đó: \(\left(a-b\right)\left(b-c\right)\ge0\)

\(\Leftrightarrow ab+bc\ge ac+b^2\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{c}+1\ge\dfrac{a}{b}+\dfrac{b}{c}\\\dfrac{c}{a}+1\ge\dfrac{c}{b}+\dfrac{b}{a}\end{matrix}\right.\)

\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le2+2\left(\dfrac{a}{c}+\dfrac{c}{a}\right)\)

Vì \(1\le c\le a\le2\Rightarrow\left(\dfrac{a}{c}-2\right)\left(\dfrac{2a}{c}-1\right)\le0\)

\(\Leftrightarrow\dfrac{a}{c}+\dfrac{c}{a}\le\dfrac{5}{2}\)

\(\Rightarrow\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}+\dfrac{b}{a}+\dfrac{c}{b}+\dfrac{a}{c}\le7\)

\(\Leftrightarrow\left(a+b+c\right)\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le10\)

Đẳng thức xảy ra khi \(a=b=2;c=1\) và các hoán vị.