Cho phương trình ax2 + bx + c = 0 có 2 nghiệm x1 , x2 thuộc [0;1]. Chứng minh rằng:
\(M=\frac{\left(a-b\right)\left(2a-b\right)}{a\left(a-b+c\right)}\le3\)
Những câu hỏi liên quan
Cho phương trình ax2 + bx + c = 0 ( a ≠ 0 ) có hai nghiệm phân biệt x1, x2thoả x1 = x2^2 . Chứng minh b3 + a 2c + ac 2 = 3abc
theo bài ra ta có
n = 8a +7=31b +28
=> (n-7)/8 = a
b= (n-28)/31
a - 4b = (-n +679)/248 = (-n +183)/248 + 2
vì a ,4b nguyên nên a-4b nguyên => (-n +183)/248 nguyên
=> -n + 183 = 248d => n = 183 - 248d (vì n >0 => d<=0 và d nguyên )
=> n = 183 - 248d (với d là số nguyên <=0)
vì n có 3 chữ số lớn nhất => n<=999 => d>= -3 => d = -3
=> n = 927
Đúng 0
Bình luận (0)
sao 2 thằng giải trên giống trong yahoo hỏi đáp vậy
Đúng 0
Bình luận (0)
Cho phuong trình bậc hai ax2 + bx+ c =0 có hai nghiệm x1,x2 deu khác 0 . Phương trình bậc hai nhận 2x1 và 2x2 làm nghiệm là:
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
Đúng 0
Bình luận (0)
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
3x2 + 8x + 2
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
Đúng 0
Bình luận (0)
Chọn phát biểu đúng: Phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+...
Đọc tiếp
Chọn phát biểu đúng: Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = − b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = − b a x 1 . x 2 = − c a
D. x 1 + x 2 = b a x 1 . x 2 = − c a
Cho phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) . Nếu x 1 ; x 2 là hai nghiệm của phương trình thì x 1 + x 2 = − b a x 1 . x 2 = c a
Đáp án: A
Đúng 0
Bình luận (0)
Chứng tỏ rằng nếu phương trình
a
x
2
+
b
x
+
c
0
có nghiệm là
x
1
v
à
x
2
thì tam thức
a
x
2
+
b
x
+...
Đọc tiếp
Chứng tỏ rằng nếu phương trình a x 2 + b x + c = 0 có nghiệm là x 1 v à x 2 thì tam thức a x 2 + b x + c phân tích được thành nhân tử như sau:
a x 2 + b x + c = a ( x - x 1 ) ( x - x 2 )
Áp dụng : phân tích đa thức thành nhân tử.
a ) 2 x 2 - 5 x + 3 ; b ) 3 x 2 + 8 x + 2
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
Đúng 0
Bình luận (0)
Chọn phát biểu đúng. Phương trình
a
x
2
+
b
x
+
c
(
a
≠
0
)
có hai nghiệm
x
1
;
x
2
. Khi đó: A.
x
1
+
x...
Đọc tiếp
Chọn phát biểu đúng. Phương trình a x 2 + b x + c ( a ≠ 0 ) có hai nghiệm x 1 ; x 2 . Khi đó:
A. x 1 + x 2 = - b a x 1 . x 2 = c a
B. x 1 + x 2 = b a x 1 . x 2 = c a
C. x 1 + x 2 = - b a x 1 . x 2 = - c a
D. x 1 + x 2 = b a x 1 . x 2 = - c a
Đáp án A
Cho phương trình bậc hai a x 2 + b x + c ( a ≠ 0 ) .
Nếu x 1 ; x 2 là hai nghiệm của phương trình thì:
Đúng 0
Bình luận (0)
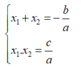
Chứng tỏ rằng nếu phương trình ax2 + bx + c = 0 có nghiệm là x1 và x2 thì tam thức ax2 + bx + c phân tích được thành nhân tử như sau:
ax2 + bx + c = a( x - x1)(x - x2)
Áp dụng : phân tích đa thức thành nhân tử.
2x2 - 5x + 3
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: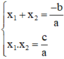 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
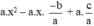
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm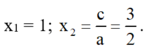 
Vậy: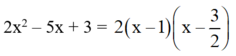 
Đúng 0
Bình luận (0)
cho phương trình ax2 + bx + c = 0 vô nghiệm ( a>0)
CMR: ax2 + bx + c > 0 với mọi x thuộc R
Vì PTVN nên Δ<0
=>f(x)=ax^2+bx+c luôn cùng dấu với a
=>f(x)>0 với mọi x
Đúng 0
Bình luận (0)
Cho phương trình bậc hai: ax2+bx+c=0 có hai nghiệm x1,x2thỏa mãn ax1+bx2+c=0. Tính M=a2c+ac2+b3-3abc+2018
Chứng minh rằng nếu phương trình a
x
2
+ bx + c x (a
≠
0) vô nghiệm thì phương trình a
a
x
2
+
b
x
+
c
2
+ b(a...
Đọc tiếp
Chứng minh rằng nếu phương trình a x 2 + bx + c = x (a ≠ 0) vô nghiệm thì phương trình a a x 2 + b x + c 2 + b(a x 2 + bx + c) + c = x cũng vô nghiệm.
