Mặt phẳng đi qua điểm A(1;1;1) và vuông
góc với hai mặt phẳng x + y - z -2 = 0,
x + y + z - 1 = 0 có phương trình là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho điểm A(1;-1;2) và mặt phẳng (P): 2x-y+z+1=0. Mặt phẳng (Q) đi qua điểm A và song song với (P). Phương trình mặt phẳng (Q) là:
![]()
![]()
![]()
![]()
Cho điểm A không thuộc đường thẳng d. Lấy hai điểm phân biệt B và C thuộc đường thẳng d (Hình 18).
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
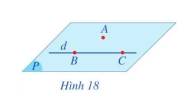
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d
Trong không gian Oxyz, cho hai điểm A ( 2 ; - 1 ; 4 ) , B ( 3 ; 2 ; - 1 ) và mặt phẳng (P): x + y + 2 z - 4 = 0 . Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phuơng trình là
A. 11 x − 7 y − 2 z + 21 = 0
B. 11 x + 7 y - 2 z - 7 = 0
C. 11 x - 7 y - 2 z - 21 = 0
D. 11 x + 7 y - 2 z + 7 = 0
Trong không gian với hệ tọa độ Oxyz cho điểm \ A 1 ; - 1 ; 2 và mặt phẳng P : 2 x - y + z + 1 = 0 . Mặt phẳng (Q) đi qua điểm A và song song với (P). Phương trình mặt phẳng (Q) là
A. 2 x - y + z = 0
B. x + y + z - 2 = 0
C. 2 x + y - z + 1 = 0
D. 2 x - y + z - 5 = 0
Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2 ;-1 ;3) và song song với mặt phẳng (Q): 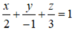
A. ![]()
B. x - 2y + 3z - 15 = 0
C. 3x - 6y + 2z - 18 = 0
D. 3x - 6y + 2z + 18 = 0
Đáp án C
Phương trình mặt phẳng (Q) viết lại dưới dạng: 3x - 6y + 2z - 6 = 0
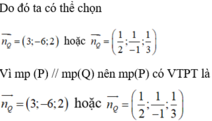
Suy ra đáp án B sai. Trong ba đáp án còn lại chỉ có mặt phẳng ở đáp án C đi qua điểm A.
Cho tứ diện A1A2A3A4. Xét 6 mặt phẳng, mỗi mặt phẳng đi qua trung điểm của một cạnh và vuông góc với cạnh đối diện.
a) Chứng minh rằng 6 mặt phẳng này cùng đi qua một điểm M. (Điểm này được gọi là điểm "Monge" của hình tứ diện A1A2A3A4)
b) CMR \(\left\{{}\begin{matrix}\overrightarrow{MA_1}.\overrightarrow{MA_2}=\overrightarrow{MA_3}.\overrightarrow{MA_4}\\\overrightarrow{MA_1}.\overrightarrow{MA_3}=\overrightarrow{MA_2}.\overrightarrow{MA_4}\\\overrightarrow{MA_1}.\overrightarrow{MA_4}=\overrightarrow{MA_2}.\overrightarrow{MA_3}\end{matrix}\right.\)
c) Giả sử M nằm trện một mặt bất kì của tứ diện. CMR chân đường cao ứng với mặt đó nằm trên đường tròn ngoại tiếp của mặt đó.
Cho các phát biểu sau, số phát biểu đúng:
1. Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt
2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt
3. Nếu 1 đường thẳng có 1 điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó
4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng
5. Tồn tại 4 điểm cùng thuộc một mặt phẳng
6. Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng sẽ còn 1 điểm chung khác
7. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng có thể không đúng
A. 3
B. 4
C. 5
D. 6
Đáp án B
Các phát biểu đúng: 1; 4; 5; 6
2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt không thẳng hàng
3. Nếu 1 đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó
7. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng
Mặt phẳng (P) đi qua hai điểm A(1;1;2), B(-4;2;1) và vuông góc với mặt phẳng (Q): 2x - 5y + 1 = 0 có phương trình là
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Trong không gian Oxyz mặt phẳng đi qua ba điểm A (1;2;2), B (3;-3;-1), C (-1;0;2) và mặt phẳng (P): 2x + y - 2z - 1= 0 Xét là điểm thay đổi thuộc mặt phẳng (P) giá trị nhỏ nhất của | M A ⇀ + 2 M B ⇀ + 3 M C ⇀ bằng:
A. 8 3
B. 5 3
C. 10 3
D. 9
Lập phương trình mặt phẳng ( α ) đi qua hai điểm A(0; 1; 0) , B(2; 3; 1) và vuông góc với mặt phẳng ( β ): x + 2y – z = 0 .
Mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng ( β ): x + 2y – z = 0.
Vậy hai vecto có giá song song hoặc nằm trên ( α ) là AB → = (2; 2; 1) và n β → = (1; 2; −1).
Suy ra ( α ) có vecto pháp tuyến là: n α → = (−4; 3; 2)
Vậy phương trình của ( α ) là: -4x + 3(y – 1) + 2z = 0 hay 4x – 3y – 2z + 3 = 0