Tính khoảng cách từ điểm \(M\left(1;2;0\right)\) lần lượt đến các mặt phẳng sau :
a) \(\left(\alpha\right):x+2y-2z+1=0\)
b) \(\left(\beta\right):3x+4z+25=0\)
c) \(\left(\gamma\right):z+5=0\)
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
Tính khoảng cách từ điểm \(M\left( {1;2} \right)\) đến đường thẳng\(\Delta :\left\{ \begin{array}{l}x = 5 + 3t\\y = - 5 - 4t\end{array} \right.\).
Ta có:
\(\left\{ {\begin{array}{*{20}{l}}
{x = 5 + 3t}\\
{y = - 5 - 4t}
\end{array}} \right. \Rightarrow 4x + 3y = 4(5 + 3t) + 3( - 5 - 4t) = 5\)
Phương trình tổng quát của \(\Delta \) là \(4x + 3y - 5 = 0\)
Khoảng cách từ M đến đường thẳng \(\Delta \) là \(d\left( {M,\Delta } \right) = \frac{{\left| {4.1 + 3.2 - 5} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 1\).
Cho hình chóp \(S.ABCD\) với đáy \(ABCD\) là hình vuông cạnh \(a\). Cho biết \(SA = a\) và \(SA\) vuông góc với \(\left( {ABCD} \right)\).
a) Tính khoảng cách từ điểm \(B\) đến \(\left( {SAD} \right)\).
b) Tính khoảng cách từ điểm \(A\) đến cạnh \(SC\).
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow AB \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\end{array}\)
b) Kẻ \(AH \bot SC \Rightarrow d\left( {A,SC} \right) = AH\)
Tam giác \(ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \)
Tam giác \(SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
Tam giác \(SAC\) vuông tại \(A\) có đường cao \(AH\)\( \Rightarrow AH = \frac{{SA.AC}}{{SC}} = \frac{{a\sqrt 6 }}{3}\)
Vậy \(d\left( {A,SC} \right) = \frac{{a\sqrt 6 }}{3}\).
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng √2 lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$
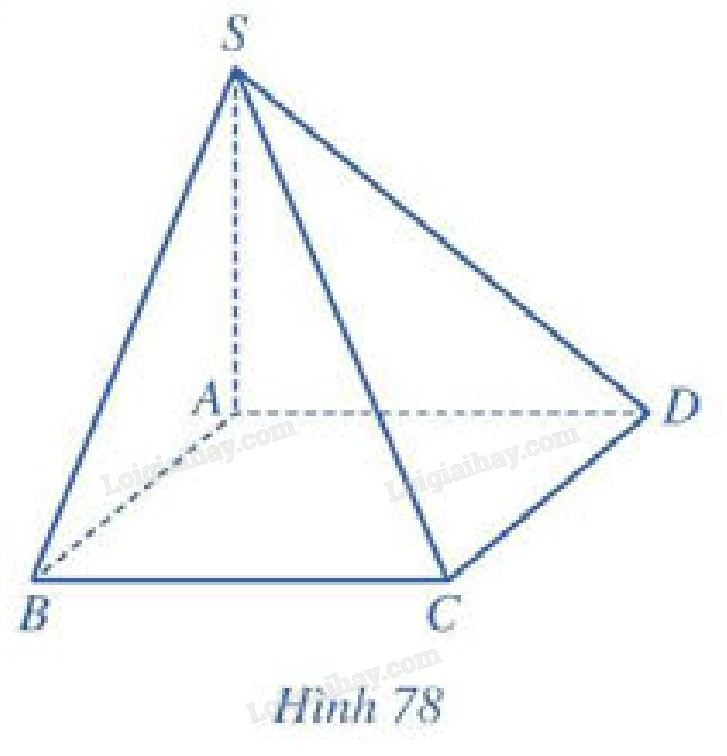
Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(a\), \(SA = a\) (Hình 78).
a) Tính khoảng cách từ điểm \(S\) đến đường thẳng \(C{\rm{D}}\).
b) Tính khoảng cách từ điểm \(D\) đến mặt phẳng \(\left( {SAB} \right)\).
c) Tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SCD} \right)\).
a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot C{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{D}} \bot C{\rm{D}}\)
\(\begin{array}{l} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot S{\rm{D}}\\ \Rightarrow d\left( {S,C{\rm{D}}} \right) = S{\rm{D}} = \sqrt {S{A^2} + A{{\rm{D}}^2}} = a\sqrt 2 \end{array}\)
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot A{\rm{D}}\)
\(ABCD\) là hình vuông \( \Rightarrow A{\rm{B}} \bot A{\rm{D}}\)
\( \Rightarrow A{\rm{D}} \bot \left( {SA{\rm{B}}} \right) \Rightarrow d\left( {D,\left( {SAB} \right)} \right) = A{\rm{D}} = a\)
c) Kẻ \(AH \bot S{\rm{D}}\left( {H \in S{\rm{D}}} \right)\).
\(C{\rm{D}} \bot \left( {SA{\rm{D}}} \right) \Rightarrow C{\rm{D}} \bot AH\)
\( \Rightarrow AH \bot \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = AH\)
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AH\)
\( \Rightarrow AH = \frac{{SA.A{\rm{D}}}}{{S{\rm{D}}}} = \frac{{a\sqrt 2 }}{2}\)
Vậy \(d\left( {A,\left( {SC{\rm{D}}} \right)} \right) = \frac{{a\sqrt 2 }}{2}\).
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
tìm m để đồ thị hàm số \(\left(C_m\right):y=x^3-3mx^2+3\left(m^2-1\right)x-m^3+m\) có cực trị đồng thời khoảng cách từ điểm cực đại của đồ thị hàm số O bằng \(\sqrt{2}\) lần khoảng cách từ điểm cực tiểu của đồ thị hàm số đến O ( O là gốc tọa độ )
Trong mặt phẳng Oxy, cho đường tròn (C): \(\left(x-1\right)^2+y^2=2\) và đường thẳng \(\Delta:x-y+4=0\) gọi \(M\left(x_0;y_0\right)\) \(\in\) (C) là điểm có khoảng cách từ m tới (\(\Delta\)) lớn nhất. Tính \(x_0+y_0\)
: Kinh độ của 1 điểm là
A. khoảng cách tính bằng độ từ điểm đó đến xích đạo.
B. khoảng cách tính bằng độ từ điểm đó đến cực.
C. khoảng cách tính bằng độ từ điểm đó đến vĩ tuyến đi qua điểm đó.
khoảng cách tính bằng độ từ kinh tuyến gốc đến kinh tuyến đi qua điểm đó
1.Một ô tô chạy từ A đến B với vận tốc 65km/h, cùng lúc đó 1 xe máy chạy từ B đến A với vận tốc 40km/h.Biết khoảng cách AB là 540km và M là trung điểm của AB.Hỏi sau khi khổi hành bao nhiêu thì ô tô cách M một khoảng bằng 1/2 khoảng cách từ xe máy đến M
2.Tính:
B = 1 + \(\frac{1}{2}\left(1+2\right)+\frac{1}{3}\left(1+2+3\right)+\frac{1}{4}\left(1+2+3+4\right)+...+\frac{1}{20}\left(1+2+3+...+20\right)\)
3.Độ dài 3 cạnh của tam giác tỉ lệ với 2;3;4.Hỏi 3 chiều cao tương ứng 3 cạnh đó tỉ lệ với số nào?
Bài 1:
Nửa quãng đường AB( hay M cách A, B) dài là:
540:2=270(km)
Gọi quãng đường ô tô và xe máy đã đi lần lượt là S1; S2 (km) và t (giờ) là thời gian cần tìm.
Trong cùng 1 thời gian đi thì quãng đường tỉ lệ thuận với vận tốc.
\(\Rightarrow\frac{S_1}{65}=\frac{S_2}{40}=t\)
Ta có:
\(S_1=\frac{1}{2}\cdot S_2\)
\(\Rightarrow t=\frac{270-a}{65}=\frac{540-2a}{130}=\frac{270-2a}{40}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(t=\frac{540-2a}{130}=\frac{270-2a}{40}=\frac{\left(540-2a\right)-\left(270-2a\right)}{130-40}=\frac{270}{90}=3\)
Vậy sau khi khởi hành 3 giờ thì ô tô cách M 1 khoảng bằng \(\frac{1}{2}\) khoảng cách từ xe máy đến M.