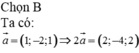Trong không gian Oxyz, cho các vectơ a→(1;−1;0),b→(−1;1;2), c→(1;−2;−1), d→(1;0;0) và d→=ma→−nb→+pc→, khi đó giá trị của m,n,p là:

Những câu hỏi liên quan
Trong không gian Oxyz , cho vectơ
a
⇀
(2; 1; -2). Tìm tọa độ của các vectơ
b
⇀
cùng phương với vectơ
a
⇀
và có độ dài bằng 6. A.
b
⇀
4
;
2
;
-
4
B. ...
Đọc tiếp
Trong không gian Oxyz , cho vectơ a ⇀ = (2; 1; -2). Tìm tọa độ của các vectơ b ⇀ cùng phương với vectơ a ⇀ và có độ dài bằng 6.
A. b ⇀ = 4 ; 2 ; - 4
B. b ⇀ = - 4 ; - 2 ; 4
C. b ⇀ = 4 ; 2 ; - 4 hoặc b ⇀ = - 4 ; - 2 ; 4
D. b ⇀ = 12 ; 6 ; - 12 hoặc b ⇀ = - 12 ; - 6 ; 12
Đáp án C
Ta có:
![]()
Mặt khác hai vectơ này cùng phương nên ta có:
![]()
Từ đó ta suy ra
![]()
Lưu ý. Đáp án D là sai, do sai lầm trong tính độ dài của vectơ a ⇀
![]()
Mà hai vectơ này cùng phương nên ta có:
![]()
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho
u
→
1
;
−
2
;
3
. Trong các vectơ sau, đâu là vectơ vuông góc với vectơ
u
→
? A.
a
→
2
;
−
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho u → = 1 ; − 2 ; 3 . Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?
A. a → = 2 ; − 4 ; 6 .
B. b → = 0 ; 3 ; − 2 .
C. c → = − 1 ; 1 ; − 1 .
D. d → = 2 ; 4 ; 2 .
Trong không gian với hệ tọa độ Oxyz, cho
u
→
(
1
;
−
2
;
3
)
. Trong các vectơ sau, đâu là vectơ vuông góc với vectơ
u
→
? A.
a
→
(
2
;
−
4
;
6
)
B.
b
→
(
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho u → = ( 1 ; − 2 ; 3 ) . Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?
A. a → = ( 2 ; − 4 ; 6 )
B. b → = ( 0 ; 3 ; − 2 )
C. c → = ( − 1 ; 1 ; − 1 )
D. d → = ( 2 ; 4 ; 2 )
Trong không gian với hệ tọa độ Oxyz, cho
u
→
(1;-2;3). Trong các vectơ sau, đâu là vectơ vuông góc với vectơ
u
→
?
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho u → = (1;-2;3).
Trong các vectơ sau, đâu là vectơ vuông góc với vectơ u → ?
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho mặt phẳng
P
:
3
x
-
y
+
z
+
1
0
. Trong các vectơ sau, vectơ nào không phải là vectơ pháp tuyến của mặt phẳng (P)? A.
n
1
→
-
3
;
-
1
;
-...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng P : 3 x - y + z + 1 = 0 . Trong các vectơ sau, vectơ nào không phải là vectơ pháp tuyến của mặt phẳng (P)?
A. n 1 → = - 3 ; - 1 ; - 1
B. n 4 → = 6 ; - 2 ; 2
C. n 3 → = - 3 ; 1 ; - 1
D. n 2 → = 3 ; - 1 ; 1
Trong không gian Oxyz cho vectơ
a
→
(
1
;
-
2
;
1
)
. Vectơ
2
a
→
có tọa độ là
Đọc tiếp
Trong không gian Oxyz cho vectơ a → = ( 1 ; - 2 ; 1 ) . Vectơ 2 a → có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho các điểm
A
(
2
;
-
2
;
1
)
,
B
(
1
;
-
1
;
3
)
. Tọa độ của vectơ
A
B
→
là A. (1;-1;-2) B. (-1;1;2) C. (3;-3;4) D. (-3;3;-4)
Đọc tiếp
Trong không gian Oxyz, cho các điểm A ( 2 ; - 2 ; 1 ) , B ( 1 ; - 1 ; 3 ) . Tọa độ của vectơ A B → là
A. (1;-1;-2)
B. (-1;1;2)
C. (3;-3;4)
D. (-3;3;-4)
Trong không gian với hệ tọa độ Oxyz, cho các vectơ
a
→
2
;
m
-
1
;
3
,
b
→
1
;
3
;
-
2
n
. Tìm m, n để các vectơ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các vectơ a → = 2 ; m - 1 ; 3 , b → = 1 ; 3 ; - 2 n . Tìm m, n để các vectơ a → , b → cùng hướng
A. m = 7 , n = - 3 4
B. m = 1 , n = 0
C. m = 7 , n = - 4 3
D. m = 4 , n = - 3
Trong không gian với hệ tọa độ Oxyz, cho các vectơ
a
→
2
;
m
-
1
;
3
,
b
→
1
;
3
;
-
2
n
. Tìm m, n để các vectơ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các vectơ a → = 2 ; m - 1 ; 3 , b → = 1 ; 3 ; - 2 n . Tìm m, n để các vectơ a → , b → cùng hướng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho các vectơ
a
→
(2;m-1;3),
b
→
(1;3;-2n). Tìm m, n để các vectơ
a
→
,
b
→
cùng hướng.
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các vectơ a → = (2;m-1;3), b → = (1;3;-2n). Tìm m, n để các vectơ a → , b → cùng hướng.
![]()
![]()
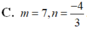
![]()